The mill
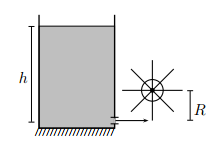
Water from a reservoir is used to rotate a mill of radius R with angular velocity ω constant through the jet flowing from the orifice of area S situated at a depth h of its level. With the jet perpendicularly incident on each shovel, with totally inelastic shock, calculate the torque of the friction forces on the mill axis, where ρ and g, respectively, are the mass, specific gravity and acceleration of gravity.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
According to energy conservation, the speed at which water exits the reservoir is given by v = √2gh After the inelastic shock, a portion of the water with mass Δm will have velocity ωR. Being thus, the linear momentum variation of this water mass will be given by Δp = Δm ⋅ (v - ω R).
To determine the mass of water reaching one of the blades in a time interval Δt, we will consider a cylindrical portion that emerges from the hole with area of the base S and length L. The mass contained in this cylinder is given by Δm = ρ ⋅ S ⋅ L. Note that after a time interval Δt the blade shifts ωRΔt. Therefore, the length of the cylinder that reaches the blade is given by L = (v - ω R) Δt. Therefore the mass of the cylinder will be: Δm = ρS (v - ω R) Δt Thus, the average force applied by the water on a shovel of the mill is given by:
F = Δ t Δ p = ρS(v – ωR)²
F = = ρSv²(1- v ω R )²
The torque of the friction forces has the same modulus of the torques of the water portion that hits the shovel, then:
M = R ⋅ F = ρSv²R(1- v ω R )²
M = 2ρghRS(1- √ 2 g h ω R )²