An algebra problem by Aly Ahmed

The question is actually to find the minimum value of the sum of distances of two line segments joining points $(0,x-3),(2,0)$ and points $(2,0),(4,-x)$ . Obviously, the minimum value of this is the straight line distance between points $(0,x-3),(4,-x)$ when the points $(0,x-3),(2,0),(4,-x)$ are collinear. That is,

$x-3=-x\implies x=1.5$ .

Then the minimum distance will be

$\sqrt {(0-4)^2+(-1.5-1.5)^2}=\boxed 5$ .

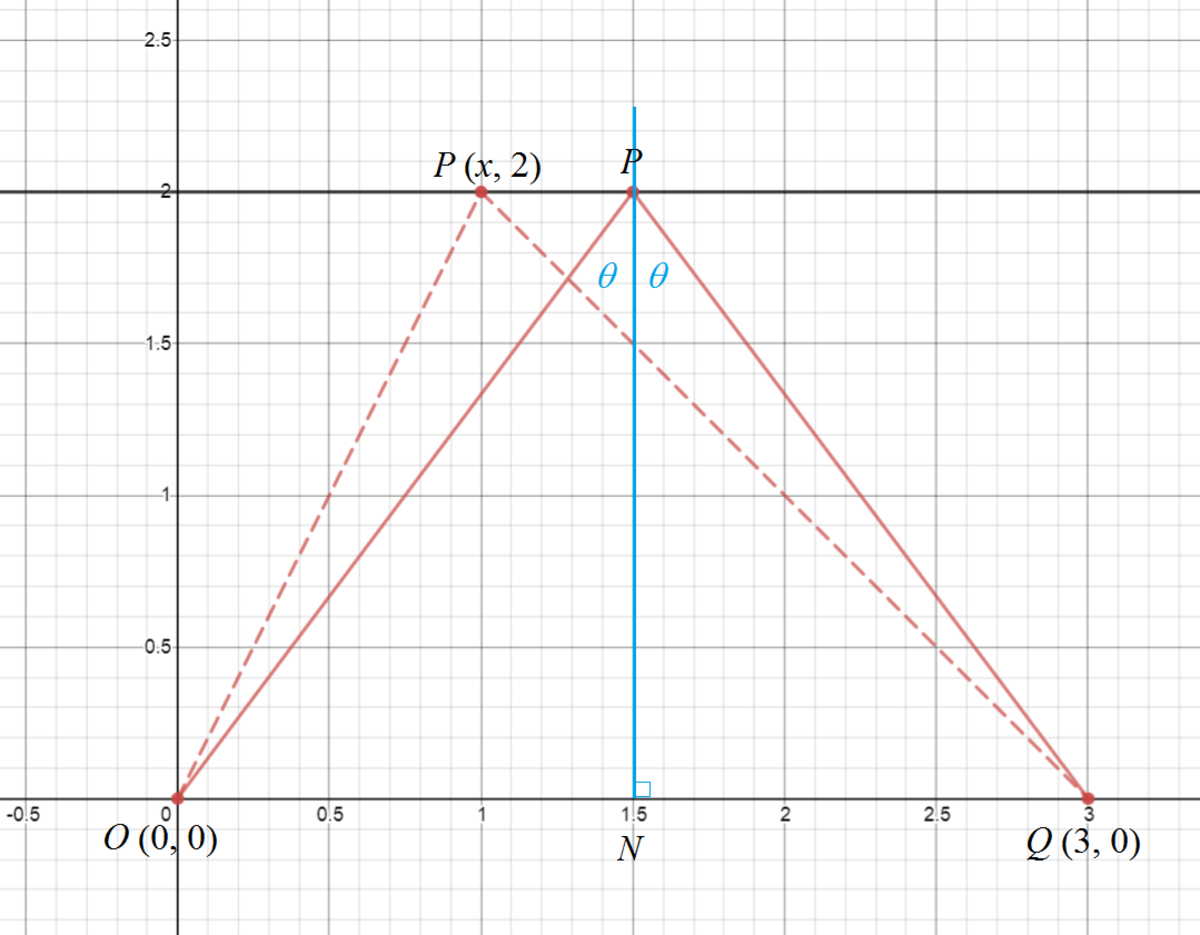
Note that $\sqrt{x^2+4} + \sqrt{x^2-6x+13} = \sqrt{(x-0)^2+(2-0)^2} + \sqrt{(x-3)^2 + (2-0)^2}$ is equivalent to the sum of lengths of $OP$ and $PQ$ , where $O(0,0)$ , $Q(3,0)$ , and $P(x,2)$ is a point on $y=2$ . The shortest distance to get from $O$ to $Q$ via $P$ is the same as that traveled by light from $O$ to $Q$ reflected at $P$ , as if $y=2$ is a mirror. Then the angles of incident and reflection are the same or $\angle OPN = \angle QPN$ , where $PN$ is normal to the mirror $y=2$ . Therefore $\min \left(\sqrt{x^2+4} + \sqrt{x^2-6x+13}\right) = 2\sqrt{ON^2+PN^2} = 2 \times \sqrt{1.5^2+2^2} = \boxed 5$ .