The minimal
Find the square of the minimum value of 9 + x 2 + ( 4 − x ) 2 + ( 3 − y ) 2 + 4 + y 2 as x and y range over all real numbers.
The answer is 72.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Brilliant! This is a very simple and elegant solution. Thanks for sharing this approach, Harry :)
9 + x 2 + ( 4 − x ) 2 + ( 3 − y ) 2 + 4 + y 2
Using Cauchy-Schwarz in Titu form,
( 1 2 + 1 2 ) ( 3 2 + x 2 ) ≥ ( 3 + x ) 2
9 + x 2 ≥ 2 ( 3 + x ) 2
9 + x 2 ≥ 2 x + 3
Similarly,
( 4 − x ) 2 + ( 3 − y ) 2 ≥ 2 7 − x − y
4 + y 2 ≥ 2 y + 2
Adding all these inequalities,
9 + x 2 + ( 4 − x ) 2 + ( 3 − y ) 2 + 4 + y 2 ≥ 2 x + 3 + 2 7 − x − y + 2 y + 2
9 + x 2 + ( 4 − x ) 2 + ( 3 − y ) 2 + 4 + y 2 ≥ 2 1 2
≥ 6 2
Hence, the answer is 7 2
Same , But just for sake of variety , I used the fact that RMS value is always greater than the average value. And I think all of us Proved it in our schools , In while studying A l t e r n a t i n g C u r r e n t chapter (Otherwise we can also proove it by using 2-D co-ordinate geometry , i.e by using s t r a i g h t L i n e s ). Hence :
R m s ≥ A v g 2 a 2 + b 2 ≥ 2 a + b a 2 + b 2 ≥ 2 a + b
So Applying This concept on this question , we get 9 + x 2 + ( 4 − x ) 2 + ( 3 − y ) 2 + 4 + y 2 ≥ 2 1 2
Equality Occurs , Means Minimum is achieve when values becomes equal on which we are doing Inspection . Means when a = b .
Hence x = 3 , y = 2 .
can u explain it a bit further??
Let us represent the given expression by f ( x , y ) , and then, f ( x , y ) = ∣ 3 i + x j ∣ + ∣ ( 4 − x ) i + ( 3 − y ) j ∣ + ∣ 2 i + y j ∣ . Using the triangle inequality and the inequality a 2 + b 2 ≥ 2 ( a + b ) 2 , we obtain that f ( x , y ) ≥ ∣ ( 3 + 4 − x + 2 ) i + ( x + y + 3 − y ) j ∣ = ( 9 − x ) 2 + ( x + 3 ) 2 ≥ 2 ( 9 − x + x + 3 ) 2 = 7 2 .
Besides that, all the quantities involved in these two consecutive inequalities become equal when x = 3 , and y = 2 . Then, the minimum value of f ( x , y ) for any positive values of x and y is 7 2 . Then the answer to the question is 7 2 . So, in my opinion, the condition that the values of x and y are positive is not necessary.
its easy to do in complex number system,
Relevant wiki: Classical Inequalities
I came across this problem in the geometry section, so I thought I'd provide a geometric solution.
The sum of square root terms suggests three straight-line segments. Consider the following diagram: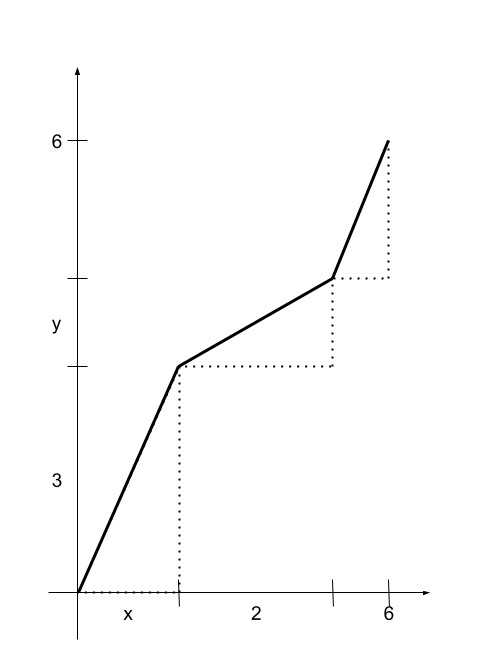 The first line segment has length
x
2
+
9
, the second has length
y
2
+
4
, and the final segment has length:
(
6
−
(
x
+
2
)
)
2
+
(
6
−
(
y
+
3
)
)
2
=
(
4
−
x
)
2
+
(
3
−
y
)
2
That is, the quantity we want to minimize is simply the sum of the lengths of these three line segments. This is minimized when they form a straight line from the origin to
(
6
,
6
)
, which has a length of
6
2
hence the answer is
7
2
.
The first line segment has length
x
2
+
9
, the second has length
y
2
+
4
, and the final segment has length:
(
6
−
(
x
+
2
)
)
2
+
(
6
−
(
y
+
3
)
)
2
=
(
4
−
x
)
2
+
(
3
−
y
)
2
That is, the quantity we want to minimize is simply the sum of the lengths of these three line segments. This is minimized when they form a straight line from the origin to
(
6
,
6
)
, which has a length of
6
2
hence the answer is
7
2
.