The minimum distance between the figures is not 1.

Calculus Level 5

Since the figures are symmetrical in all four quadrants, the problem is to be worked in the first quadrant only, where x ≥ 0 x\geq 0 and y ≥ 0 y\geq 0 .

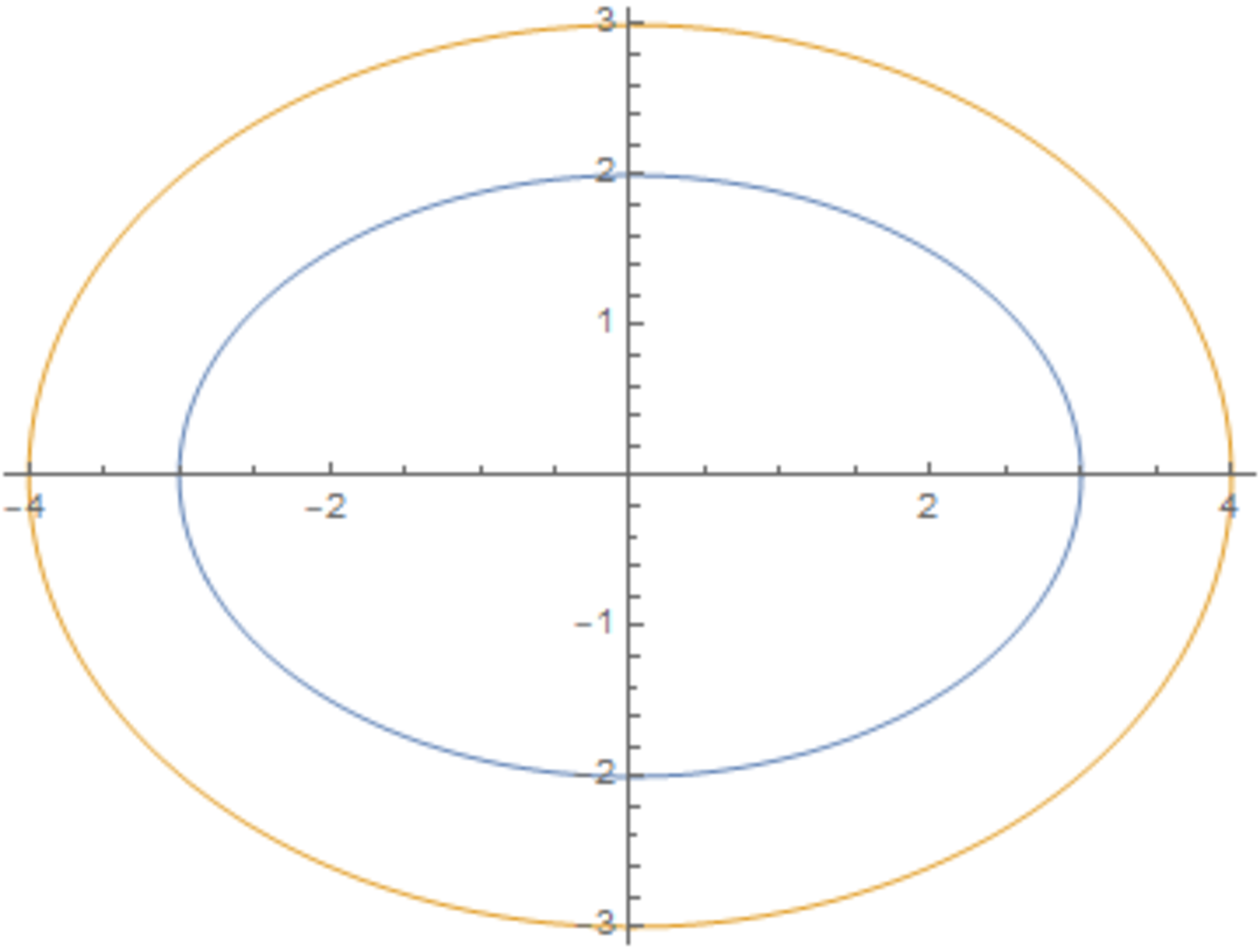
The two figures, respectively, have the equations: ( 2 x 1 ) 2 + ( 3 y 1 ) 2 = ( 2 × 3 ) 2 \left(2 x_1\right){}^2+\left(3 y_1\right){}^2=(2\times 3)^2 and ( 3 x 2 ) 2 + ( 4 y 2 ) 2 = ( 3 × 4 ) 2 \left(3 x_2\right){}^2+\left(4 y_2\right){}^2=(3\times 4)^2 .

The problem is to find the minimum distance between the figures. The answer will have the form of a relatively prime fraction possibly under a square root. The answer will be the concatenation (i.e., list altogether) of a 1 if there is no square root is required and a 2 if a square root is required, the numerator of the fraction, and the denominator of the fraction. If the answer were 47 51 \sqrt{\frac{47}{51}} and this is not the answer, then the number to be entered would be 24751. If the answer were 1 1 and this also is not the answer, then the number would be 111 because a fraction is required and in that case would be written as the answer over 1. If the answer were 19 20 \frac{19}{20} and again this is not the answer, then the number to be entered would be 11920, Last example, 999 1001 \sqrt{\frac{999}{1001}} gives 29991001.


The answer is 23435.

A Former Brilliant Member by A Former Brilliant Member

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

( 2 x 1 ) 2 + ( 3 y 1 ) 2 = ( 2 3 ) 2 ∧ x 1 ≥ 0 ∧ y 1 ≥ 0 → 0 ≤ x 1 ≤ 3 ∧ y 1 = 2 3 9 − x 1 2 \left(2 x_1\right){}^2+\left(3 y_1\right){}^2=(2\ 3)^2\land x_1\geq 0\land y_1\geq 0\to 0\leq x_1\leq 3\land y_1=\frac{2}{3} \sqrt{9-x_1^2}

( 3 x 2 ) 2 + ( 4 y 2 ) 2 = ( 3 4 ) 2 ∧ x 2 ≥ 0 ∧ y 2 ≥ 0 → 0 ≤ x 2 ≤ 4 ∧ y 2 = 3 4 16 − x 2 2 \left(3 x_2\right){}^2+\left(4 y_2\right){}^2=(3\ 4)^2\land x_2\geq 0\land y_2\geq 0\to 0\leq x_2\leq 4\land y_2=\frac{3}{4} \sqrt{16-x_2^2}

The expression for the Euclidean distance is 5 x 1 2 9 − 2 x 2 x 1 + 7 x 2 2 16 − 9 − x 1 2 16 − x 2 2 + 13 \sqrt{\frac{5 x_1^2}{9}-2 x_2 x_1+\frac{7 x_2^2}{16}-\sqrt{9-x_1^2} \sqrt{16-x_2^2}+13} .

The minimum distance is 34 35 \sqrt{\frac{34}{35}} for which the number to be entered as 23435.

Using the square of the Euclidean distance simplifies the computations and does not change the answer.

∂ ( 5 x 1 2 9 − 2 x 2 x 1 + 7 x 2 2 16 − 9 − x 1 2 16 − x 2 2 + 13 ) ∂ x 1 → 16 − x 2 2 x 1 9 − x 1 2 + 10 x 1 9 − 2 x 2 \frac{\partial \left(\frac{5 x_1^2}{9}-2 x_2 x_1+\frac{7 x_2^2}{16}-\sqrt{9-x_1^2} \sqrt{16-x_2^2}+13\right)}{\partial x_1}\to \frac{\sqrt{16-x_2^2} x_1}{\sqrt{9-x_1^2}}+\frac{10 x_1}{9}-2 x_2

∂ ( 5 x 1 2 9 − 2 x 2 x 1 + 7 x 2 2 16 − 9 − x 1 2 16 − x 2 2 + 13 ) ∂ x 2 → − 2 x 1 + 7 x 2 8 + 9 − x 1 2 x 2 16 − x 2 2 \frac{\partial \left(\frac{5 x_1^2}{9}-2 x_2 x_1+\frac{7 x_2^2}{16}-\sqrt{9-x_1^2} \sqrt{16-x_2^2}+13\right)}{\partial x_2}\to -2 x_1+\frac{7 x_2}{8}+\frac{\sqrt{9-x_1^2} x_2}{\sqrt{16-x_2^2}}

Setting the expression as being equal to 0 0 and solving the simultaneous equations with additional constraints that x 1 ≥ 0 x_1\geq 0 and x 2 ≥ 0 x_2\geq 0 gives { x 1 → 0 , x 2 → 0 } , { x 1 → 12 5 17 , x 2 → 12 5 17 } , { x 1 → 9 29 17 5 , x 2 → 16 29 17 7 } \left\{x_1\to 0,x_2\to 0\right\},\left\{x_1\to 12 \sqrt{\frac{5}{17}},x_2\to 12 \sqrt{\frac{5}{17}}\right\},\left\{x_1\to \frac{9 \sqrt{\frac{29}{17}}}{5},x_2\to \frac{16 \sqrt{\frac{29}{17}}}{7}\right\} .

Now the second derivative test is needed to determine whether any of these situations qualify.

∂ 2 ∂ x 1 ∂ x 1 ( 13 + 5 x 1 2 9 − 2 x 1 x 2 + 7 x 2 2 16 − 9 − x 1 2 16 − x 2 2 ) 16 − x 2 2 x 1 2 ( 9 − x 1 2 ) 3 / 2 + 16 − x 2 2 9 − x 1 2 + 10 9 ∂ 2 ∂ x 2 ∂ x 2 ( 13 + 5 x 1 2 9 − 2 x 1 x 2 + 7 x 2 2 16 − 9 − x 1 2 16 − x 2 2 ) 9 − x 1 2 x 2 2 ( 16 − x 2 2 ) 3 / 2 + 9 − x 1 2 16 − x 2 2 + 7 8 ∂ 2 ∂ x 1 ∂ x 2 ( 13 + 5 x 1 2 9 − 2 x 1 x 2 + 7 x 2 2 16 − 9 − x 1 2 16 − x 2 2 ) − x 1 x 2 9 − x 1 2 16 − x 2 2 − 2 \begin{array}{|c|c|} \hline \frac{\partial ^2}{\partial x_1\, \partial x_1}\left(13+\frac{5 x_1^2}{9}-2 x_1 x_2+\frac{7 x_2^2}{16}-\sqrt{9-x_1^2} \sqrt{16-x_2^2}\right) & \frac{\sqrt{16-x_2^2} x_1^2}{\left(9-x_1^2\right){}^{3/2}}+\frac{\sqrt{16-x_2^2}}{\sqrt{9-x_1^2}}+\frac{10}{9} \\ \frac{\partial ^2}{\partial x_2\, \partial x_2}\left(13+\frac{5 x_1^2}{9}-2 x_1 x_2+\frac{7 x_2^2}{16}-\sqrt{9-x_1^2} \sqrt{16-x_2^2}\right) & \frac{\sqrt{9-x_1^2} x_2^2}{\left(16-x_2^2\right){}^{3/2}}+\frac{\sqrt{9-x_1^2}}{\sqrt{16-x_2^2}}+\frac{7}{8} \\ \frac{\partial ^2}{\partial x_1\, \partial x_2}\left(13+\frac{5 x_1^2}{9}-2 x_1 x_2+\frac{7 x_2^2}{16}-\sqrt{9-x_1^2} \sqrt{16-x_2^2}\right) & -\frac{x_1 x_2}{\sqrt{9-x_1^2} \sqrt{16-x_2^2}}-2 \\ \hline \end{array}

The discriminant is ( 9 − x 1 2 x 2 2 ( 16 − x 2 2 ) 3 / 2 + 9 − x 1 2 16 − x 2 2 + 7 8 ) ( 16 − x 2 2 x 1 2 ( 9 − x 1 2 ) 3 / 2 + 16 − x 2 2 9 − x 1 2 + 10 9 ) − ( − x 1 x 2 9 − x 1 2 16 − x 2 2 − 2 ) 2 \left(\frac{\sqrt{9-x_1^2} x_2^2}{\left(16-x_2^2\right){}^{3/2}}+\frac{\sqrt{9-x_1^2}}{\sqrt{16-x_2^2}}+\frac{7}{8}\right) \left(\frac{\sqrt{16-x_2^2} x_1^2}{\left(9-x_1^2\right){}^{3/2}}+\frac{\sqrt{16-x_2^2}}{\sqrt{9-x_1^2}}+\frac{10}{9}\right)-\left(-\frac{x_1 x_2}{\sqrt{9-x_1^2} \sqrt{16-x_2^2}}-2\right){}^2 .

Evaluating the discriminant for each of the three points gives { − 1 36 , − 1445 9072 , 8381 53136 } \left\{-\frac{1}{36},-\frac{1445}{9072},\frac{8381}{53136}\right\} .

Only the last point evaluated to a positive, which is what is required for a minimization. Therefore, the minimum occurs at x 1 → 9 29 17 5 , x 2 → 16 29 17 7 x_1\to \frac{9 \sqrt{\frac{29}{17}}}{5},x_2\to \frac{16 \sqrt{\frac{29}{17}}}{7} . The cooresponding y y s are: { 4 41 17 5 , 9 41 17 7 } \left\{\frac{4 \sqrt{\frac{41}{17}}}{5},\frac{9 \sqrt{\frac{41}{17}}}{7}\right\} .

0 Helpful 0 Interesting 1 Brilliant 0 Confused
Uahnbu Tran
Oct 15, 2020

For x 1 x_1 of f ( x ) f(x) and x 2 x_2 of g ( x ) g(x) which yield the minimum distance, there shall be 2 equations:

( 1 ) f ′ ( x 1 ) = g ′ ( x 2 ) (1) f'(x_1)=g'(x_2) since slopes at intersections should be equal

( 2 ) f ( x 1 ) + x 1 f ′ ( x 1 ) = g ( x 2 ) + x 2 g ′ ( x 2 ) (2) f(x_1)+\frac{x_1}{f'(x_1)}=g(x_2)+\frac{x_2}{g'(x_2)} since y intercepts for the lines should be equal

For this problem, (1) means − 2 x 1 3 9 − x 1 2 = − 3 x 2 4 16 − x 2 2 \frac{-2x_1}{3\sqrt{9-x_1^2}}=\frac{-3x_2}{4\sqrt{16-x_2^2}}

and (2) is 7 12 16 − x 1 2 = 5 6 9 − x 2 2 \frac7{12}\sqrt{16-x_1^2}=\frac56\sqrt{9-x_2^2}

which both combined shall reduce to a quadratic equation in terms of x 1 2 x_1^2 .

The value is 9 5 29 17 \frac95\sqrt\frac{29}{17} and 16 7 29 17 \frac{16}7\sqrt\frac{29}{17} for x 1 x_1 and x 2 x_2 respectively.

Plug them into ( x 1 − x 2 ) 2 + ( 2 3 9 − x 1 2 − 3 4 16 − x 2 2 ) 2 \sqrt{\left(x_1-x_2\right)^2+\left(\frac23\sqrt{9-x_1^2}-\frac34\sqrt{16-x_2^2}\right)^2} to obtain the distance.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...