The minimum value of the maximum displacement

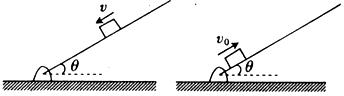As the image shows,the angle between the rough board and the horizontal ground $θ (0°≤θ≤90°)$ can change if you want. When $θ=30°$ ,a block on the board can exactly move at a constant velocity parallel to the board downwards,as the first image shows.The coefficient of kinetic friction between the rough board and the block is $μ$ .

Now let's launch the block from the bottom of the board with initial velocity $v_0= \ 10m/s$ parallel to the board upwards,as the second image shows, $x$ is the maximum displacement of the block during the movement (assuming parallel to the board upwards is positive direction) .

As angle $θ$ changes , the maximum displacement $x$ also changes. What's the minimum value of x with all possible values of angle $θ$ ? $(g=9.8m/s^2)$

Bonus :If you find the answer,find the function bewteen $x$ and $θ$ and the angle $θ$ which make $x$ minimum in your solution.