Go the distance
 Over all real numbers
x
, find the minimum value of
(
x
+
6
)
2
+
2
5
+
(
x
−
6
)
2
+
1
2
1
.
Over all real numbers
x
, find the minimum value of
(
x
+
6
)
2
+
2
5
+
(
x
−
6
)
2
+
1
2
1
.
The answer is 20.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
17 solutions
Very elegant solution ;-)
Log in to reply
Honestly Dan, did you actually devise that problem because your solution would have been difficult to work had the values of 121 and 25 not been there. Also x+6 and x-6 were helpful but turning x-6 into x-6 was really a stroke of genius which unfortunately many people failed to understand.
I guess you should send your solution to Numberphile
I dont get it
Log in to reply
theorem of pythagoras
From the Pythagorean theorem, we have AB is the first term, and BC is the second term. We can rewrite the question as asking for the minimum value of AB+ BC. To minimize this, we want AC to be a straight line. From this, we can use the Pythagorean theorem to find AC = 20.
Simplest solution bro
Don't sweat it. Same here.
Very pretty solution.
Beauty of math..
very elegant!
Lovely solution! :D
Cool. This is indeed a wise way to answer the problem.
Epic... I never thought about using geometry....
master solution
Very good solution. I seen that a lot of people didn't understand so let me shine light on this solution, in the pythagorean theorem, a^2 +b^2=c^2 , ^ means to the power of and I don"t know how to get the squared sign. Anyway substituting the fact that AB and BC are hypothenuses, AB^2= 5^2 + (6+x)^2, so thats why AB = the square root of (x+6)^2 +25. same logic gives you the same explanation for BC. This is where I assume people get confused on why AC=AB+BC. Remember the triangle inequality theorem and triangle ABC and that there would have been line AC, in this case AC<AB+BC, but we have to find the minimum value so AC=AB+BC This still technically works, it infinitely close to so it is fine. Now look in the diagram, imagine line AC existing , it is the hypothenuse of right triangle AC, and the point that is the intersection of the two sides that have lengths of 12 and 16. Using the Pythagorean theorem, AC=20, so AB+BC=20. This is quite long and I hope this helps explain the problem.
Clearing up
Added August 22 2016. A lot of people have been showing feedback on my solution so I decided to add this part. First, the two parts of the equation looked like two hypotenuses or hypoteni, as of now, August 22 2016, I realized a major issue that isn't shown how 6-x can equal to the x-6 shown in the second term, the 6-x shown in a diagram which is part of the first solution.I am going to explain why this still works.Since 6-x=-1(x-6).Replace that in the second term and -1^2 is 1 so it technically works out in the end.Anyway, after this info,I tried making a diagram, also the two sides that are integers are 5 and 11, they were squared in the two terms, they are the square root of 25 and 121. I got to make the diagram that looks just like Dan Lawson's. 6-x+6+x are two other sides in the original two terms and 6-x+6+x=12. 11+5=16 and the other leg is 12, the hypotenuse is 20. Also I edited the first part to show why we assume why AB+BC=AC.Thanks for all the feedback
No doubt it's a good explanation but can you explain what goes wrong when we interpret it in a Cartesian system ? I mean we definitely have to take the points (6,11) & (-6,5) then we have to find a point in x axis such that the above equation attains the lowest value.
Log in to reply
With that choice you have no solution. This is because no point on the x-axis intersects with the line joining (6,-11) and (-6,5) and lies between them. However, you can still solve using the cartesian approach. Try with the points (6,11) and (-6,-5). This is also valid and the intersection of this line with the x-axis gives you the solution. Hope it is clear.
Log in to reply
we can have points (6,11) and (-6,-5) we get x=-2.25 using these coordinates we get the same answer
No, one can solve it even if he takes two points A(6,11) and B(-6,5) on the cartesian plane if he has the knowledge of basic geometry and concept of image. First of all if we take P(x,0) a variable point on x axis, then we have to find the least value of PA + PB. Since A, B lies on the same side of x axis, lets take a point C (-6,-5) [ that is the image of point B in x axis to ensure that PB = PC ]. Now use the concept that the least value of PA + PC ( or PA + PB) is AC when P lies on the interior part of the line segment joining A and C. Since we know the coordinates of P and the equation of line AC, we can easily find out 'x'.
Easier to set but more difficult to solve where we ought to visualize this.
I don't get it. How can we find out the numbers of 11, 12, 16, 5, 6+x and 6-x?
Log in to reply
11 and 5 are the squared root of 25 and 121. 12 is the sum of (6+x) + (6-x).16 is 11 + 5. Just draw the two triangles and rearrange them as in the figure.
very good idea, but i think it's wrong, because we can't be sure if (x-6)>0 or (X+6) >0, we can't use this way .
Log in to reply
It doesn't matter, because all that is required is that (x-6)^2=(6-x)^2, and that is true for all real numbers .. they don't have to be positive.
Log in to reply
yes, that's right, but look at the figure, (x+6) and (x-6) are considered as two sides of the triangle, so (x+6)>0 , (x-6)>0 are the conditions! my answer is √180. The minimum value is the distance between two points A (-6, -5) and B (6, -11).
shouldn't AB be root[ (x+6)^2 +25] according to the question?
Its a joy to see such math.
really nice
Actually.... I want to know how you have the thought of taking (6-x) instead of (x-6). I didnt got the answer bacause of my traditional thinking, and was pleased by your out of box thinking!
Log in to reply
in the second term, the side could be x-6 or 6-x. we know this since (x-6)^2 is equal to (6-x)^2, double negative
That is simply genius ! :)
Beautiful solution
but i dont get how come AC is 20
Log in to reply
AC is 20 from the Pythagorean theorem, notice that a leg is 5+11 = 16, and the other is 6+x + 6-x , which is 12. This is a 3-4-5 triangle scaled up, so we have AC= 20.
please explain again. not getting it
You honestly must be a bunch of math heads, to my Simple Chef brain... what you wrote makes no sense. just being honest
That's beautiful!
https://www.geogebra.org/m/wTcucKp5
There are no references between the equation and the diagram
@Dan Lawson - I had to bash this with calculus to solve this problem. Your solution, however, is orders of magnitude more elegant. Great job!
THE BEAUTIFUL OF GEOMETRY!
This is wrong because you have ignored that x must me constant and cannot be arbitrarily placed on the line AC.
Such a nice solution...
wow nice solution
That why i love mathematics...
Nice solution
Elegant. But several of us solved for x which was not accepted as solution. Restating the problem may help
Good solution
That’s a beautiful solution. However this converts an algebra problem into a geometry problem. No wonder I struggled.
Took me a lot of time to process this solution since I didn't think of using geometry in the first place. This is great!
It is so miraculous!( •̀∀•́ )
That was a very beautiful solution, thanks a lot
@above no respect for geometry
when i saw the triangle in the question i was like what is that doing there then i see this..
I believe your answer is incorrect. Here is why. By power mean inequality, Min value is {((x+6)^2+(x-6)^2+149)^1/2} Which is(4x^2+221) Min value comes when x=0 That value is442^1/2
I think, the solution requires that [(x+6)+(x-6)]² = [(x+6)+(6-x)]² which only works for x=6 which is exactly where the original function attains its minimum =20.
Worthy question to be considered intelligent
omg that's fucking brilliant, just pure creativity
really great
Awesome man..
Off Topic : How can i draw a geometrical diagram in pc ?? Which software did you use??
Unbelievable geometrical interpretation.
Question was to find minimum value of the equation which is 24. AB + BC = AC is true for only when AB & BC are continuous straight line with same slope, for triangle or answer you have explained that should be vector AB + vector BC= vector AC. So, your answer has no logic & it is wrong.
In the figure, you switched the X's and the 6's around. When you flipped the x-6 to 6-x, it changed the whole equation
Log in to reply
Notice that -1 (x-6)= 6-x . When you square them, (6-x)^2 = (-1 (x-6))^2=(x-6)^2
Bravo! Elegant thinking.
its a beauty..
Very nicely presented.
Outstanding Solution!!!
I didnt get it ..as we know underroot is distributive if the two numbers are positive ... and both the nos. (x+6)^2 and 25 are positive nos. And similiarly 11 And (x - 6)^2 ...so it should hv been done like this . \ sqrt{ (x+6)^2 } + \sqrt{25} + \sqrt{(x-6)^2} + \sqrt{121} ......
So we get 2x + 16 ...but as it has been asked for minimim value ..there fore
2x + 16 >= 0
Therefore mimimum value of x is equal to " -8 " ..according to me ...can anyone help me clear my doubt or accept this answer
Log in to reply
Underroot is not distributive even if the two numbers are positive.
Beautiful.
very nice solution
Nice solution :-)
nice solution
if x is greater than 6 ; this method would it be true ?
Log in to reply
Yes it would still work. You can imagine point B moving away from (AC) which means AB+BC is becoming bigger and bigger.
If you read the question properly, we are not supposed to find the value of x, but find the minimum value for the given equation ( x + 6 ) 2 + 2 5 + ( x − 6 ) 2 + 1 2 1
Log in to reply
The right word would be "expression", not "equation", but you're right.
Art of the math...
one of the best answer
Your solution assumes that x-6 = 6-x... That's incorrect. The sum of the two segments is 12 only if x-6=6-x, otherwise the length of the left and right sides of the rectangle is 2x. If x-6=6-x, then x=6 and therefore you cannot use Pythagoras' theorem as x-6=0, and you can't have a triangle with 2 sides
Log in to reply
No, his solution only requires that (x-6)^2 = (6-x)^2, which is indeed true for all of the real numbers.
L e t u s d e f i n e t h e c o m p l e x n u m b e r s , z 1 = 1 1 − ( x − 6 ) i a n d z 2 = 5 + ( x + 6 ) i T h e r e f o r e , ∣ z 1 ∣ = 1 1 2 + ( x − 6 ) 2 & ∣ z 2 ∣ = 5 2 + ( x + 6 ) 2 N o w a p p l y i n g t h e t r i a n g l e i n e q u a l i t y o f c o m p l e x n u m b e r s , ∣ z 1 ∣ + ∣ z 2 ∣ ≥ ∣ z 1 + z 2 ∣ ⇒ ∣ z 1 + z 2 ∣ = 1 6 2 + 1 2 2 = 2 0 . W h i c h i s t h e m i n i m u m v a l u e .
Best Solution IMO
Thats an awesome solution!!!
I like this way.
Satisfied ... With your answer
I don't see how you prove that the function's minimum is 20. It seems to me like you just prove it to be a lower bound on the minimum...
shouldn't squaring the i on z2 have made it - (x+6)^2 ?
where did that minus sign go?
Really awsm
( x + 6 ) 2 + 2 5 is the distance between the points ( x , 3 ) and ( − 6 , 8 )
and
( x − 6 ) 2 + 1 2 1 is the distance between the points ( x , 3 ) and ( 6 , − 8 )
by Distance Formula
(This is because ( 3 − 8 ) 2 = 2 5 and ( 3 + 8 ) 2 = 1 2 1 )
Therefore, the minimum distance will be achieved if and only if all of the three points lie on the same line.
Therefore, the minimum distance is the distance between the points ( − 6 , 8 ) and ( 6 , − 8 ) which is 2 0
Whats wrong with considering the points ( x , 0 ) , ( − 6 , 5 ) and ( 6 , 1 1 ) ?
Log in to reply
I am in the same trouble. I'd like to know if someone can provide a geometric solution for that case.
Nothing is wrong! If you fix the ordinate of the point (in your case, 0) the other points change accordingly. There are infinite configurations but the final dinstance is always the same. Even in your case, the dinstance between (-6,5) and (6,11) is 20!
Actually the same. You should symmetry (-6,5) along the x axis to (-6,-5). In Chinese we call it “将军饮马问题”.
Used minima theory..... Found f(x) attains mimumum at x= -2.25. thus Solving answer=20
Point ( x , 0 ) isn't to be found between ( − 6 , 5 ) and ( 6 , 1 1 ) , therefore you cannot get minimality by Rindell Mabunga's argument. Instead of simply drawing a line, you have to apply Hero's smaller path theorem.
Log in to reply
Why??? The line between (-6,5) and (6,11) is not horizontal. So there is an interception point with horizontal axis (with coordinates (x,0))
Exactly my point!
But if we go by this method, then the three coordinates can also be assumed as (x,0), (-6,5) and (6,11). Then answer will be altogether different.
Clearest solution to me. Thanks
You need to check if you can draw a line that goes threws all this 3 points, you will get that 1 option is invalid. I did it with 1) A(0,0) 2) B(x+6,5) 3) C(12,-5)/(12,16) When I found the equation for the line I found out that the point (12,-5) can't work if I want point B to go threw line AC. so point C=(12,16). You can also try to draw it on coordinate system and see that 1 point is not logical.
best solution!
Best solution to me.😃😃😃😃
It is best solution.~!
Easiest solution for me!
I found a way but some may find it too blunt, but i rather pick this standard way when i'm stuck. (For people who couldn't approach using the solution by Dan Lawson) ;)
Just think of finding the minimum of a normal function
f
(
x
)
, we just find where
f
′
(
x
)
is 0 and there you get maximum or minimum.
Let
f
(
x
)
=
(
x
+
6
)
2
+
2
5
+
(
x
−
6
)
2
+
1
2
1
So derivative of
f
(
x
)
is
f
′
(
x
)
=
(
x
+
6
)
2
+
2
5
x
+
6
+
(
x
−
6
)
2
+
1
2
1
x
−
6
=
0
Its quite easy to solve after squaring on both sides and solving the quadratic equation
4
x
2
+
7
3
x
+
1
4
4
=
0
Roots
4
−
9
and -16,
Value of the
f
(
x
)
at the roots =
2
0
,
5
3
So Minimum value is 2 0
Moderator note:
Note that you have not shown why it is a minimum.
The roots of derevative shows extrems points. Because obviously the maximom for x is not available. The root is minimum point
Straight general way, although harder, this could be fast.
You can also show that it is minimum by taking the double derivative and seeing if it is greater than 0 or less than it, otherwise I like the way you did it. Good job ;)
No need to take 2nd derivative. It is clearly visible that no finite maxima exists, so the solution will give a minima
Best answer is the derivative test for max and min value of a function ... 👍🏻
How is -16 eliminated as a solution?
Log in to reply
If you try x=-16 on the function, the function gives =35.77, which is greater than 20 (x=-9/4), and if u graph this function, it shows only 1 minimum.
Squaring both sides can result in having more solutions then there actually are. You always have to verify your final results if you use this method and then you would indeed see that x = -16 is not an answer to the problem.
Derivative becomes zero at points of inflection. (It could be a maximum or a minimum). Usual method to find second derivative to check if its a maximum or minimum, but for this particular question there couldn't be any finite maximum as mentioned by Kaustubh.
First think graphically. It is to find a point on x-axis such that its distances from P(-6,5) and Q(6,11) add up to a minimum. And then, geometry comes in. If you prefer, it is the optics of physics. The minimum distance is the distance between P and the mirror-image of Q in x-axis, i.e.(6,-11). Now (-6-6)^2 + (5-(-11))^2 is 20^2. Hence the minimum value is 20.
Illustration provided below by Dan Lawson makes the solution clear.
but how The minimum distance is the distance between P and the mirror-image of Q in x-axis,
@Rajen Kapur - Could you please tell me how to solve these maximum-minimum, maximizing, minimizing problems... please?? I would be extremely grateful. Is there any proper/definite method to do it ...if so can you suggest some resources related to this topic? Thanks
Log in to reply
U can use calculus
I got x = 4 − 9 , − 1 6 as the critical points.
Log in to reply
Yup Yup...Calculus is fine. At that point of time :-I/E-5 months back I didnt know of critical points :P.. I was looking for something algebraic too :)
I did too. In fact, whenever I'm confronted with a maximum/minimum problem, I always resort to using calculus.
Forgot the - sign with 2.25 :l, ended up with 21.##############.. ;(
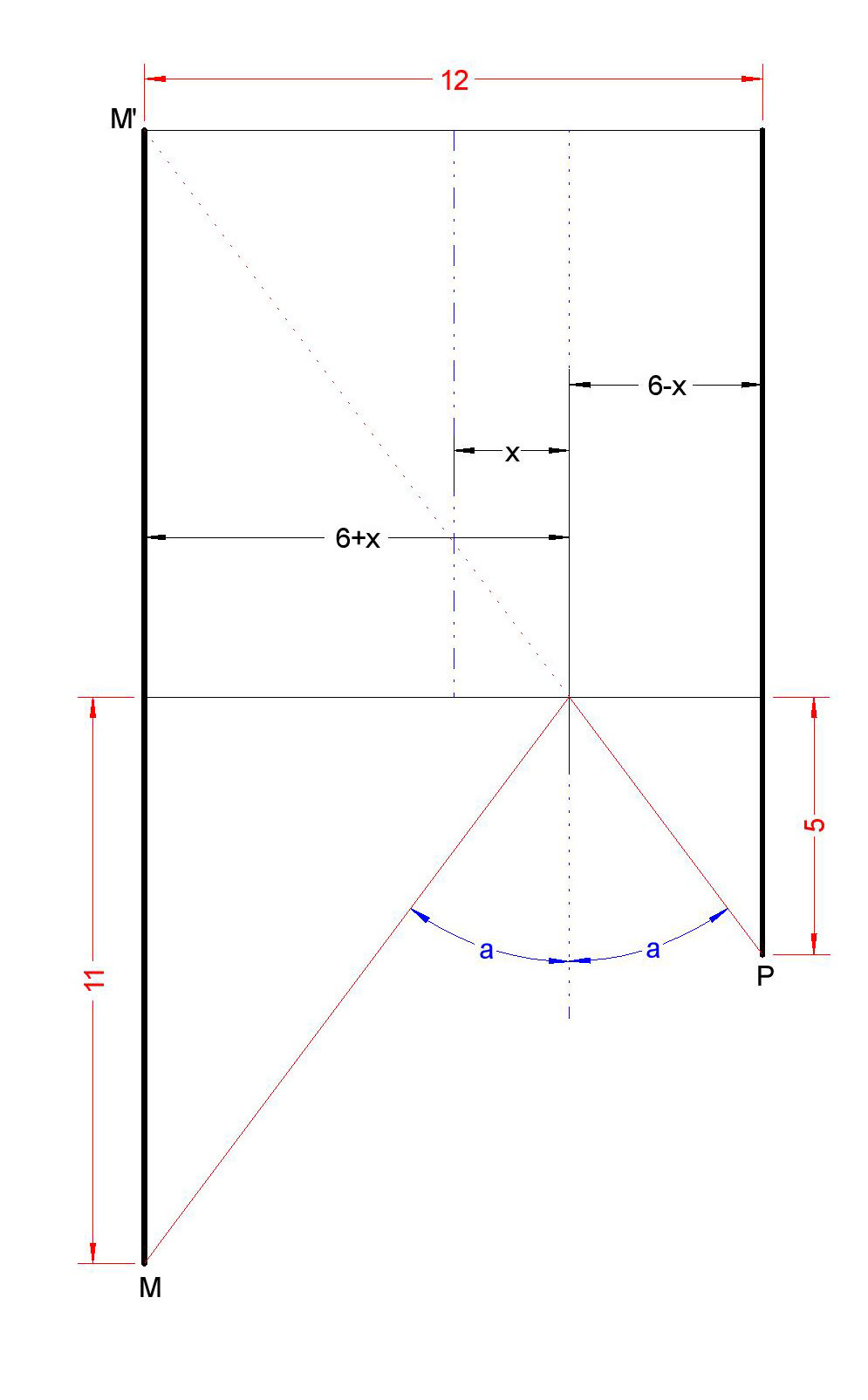
The minimum sought is the reflection of Point P into M. See the image therefore by similar triangles we get.
(6+x)/11=(6-x)/5 resolving for x we get x=2.25 and the minimum equals 2
 0
0
We can use calculus....though it will be a little bit lengthy...The 1st derivative of the function is 4x^2+73x+144....We set it to be 0 and solving for x we find x=-9/4, 16....The 2nd derivative of the function is 8x+73...plugging in -9/4 here gives lesser value than 16...so plugging -9/4 in the main function gives the minimum value and that is 20...
By the Minkowski's Inequality, ( x + 6 ) 2 + 5 2 + ( x − 6 ) 2 + 1 1 2 ≥ ( ( x + 6 ) − ( x − 6 ) ) 2 + ( 5 + 1 1 ) 2 = 2 0 .
I'll leave the equality case to be found out.
Shouldn't there be a positive sign in the rhs.
just the use of fermats principle!!
required-- distance between the points:: (-6,5) and (6,-11) for the sum to be min. which is =20
First, draw a plane coordinate system like this:
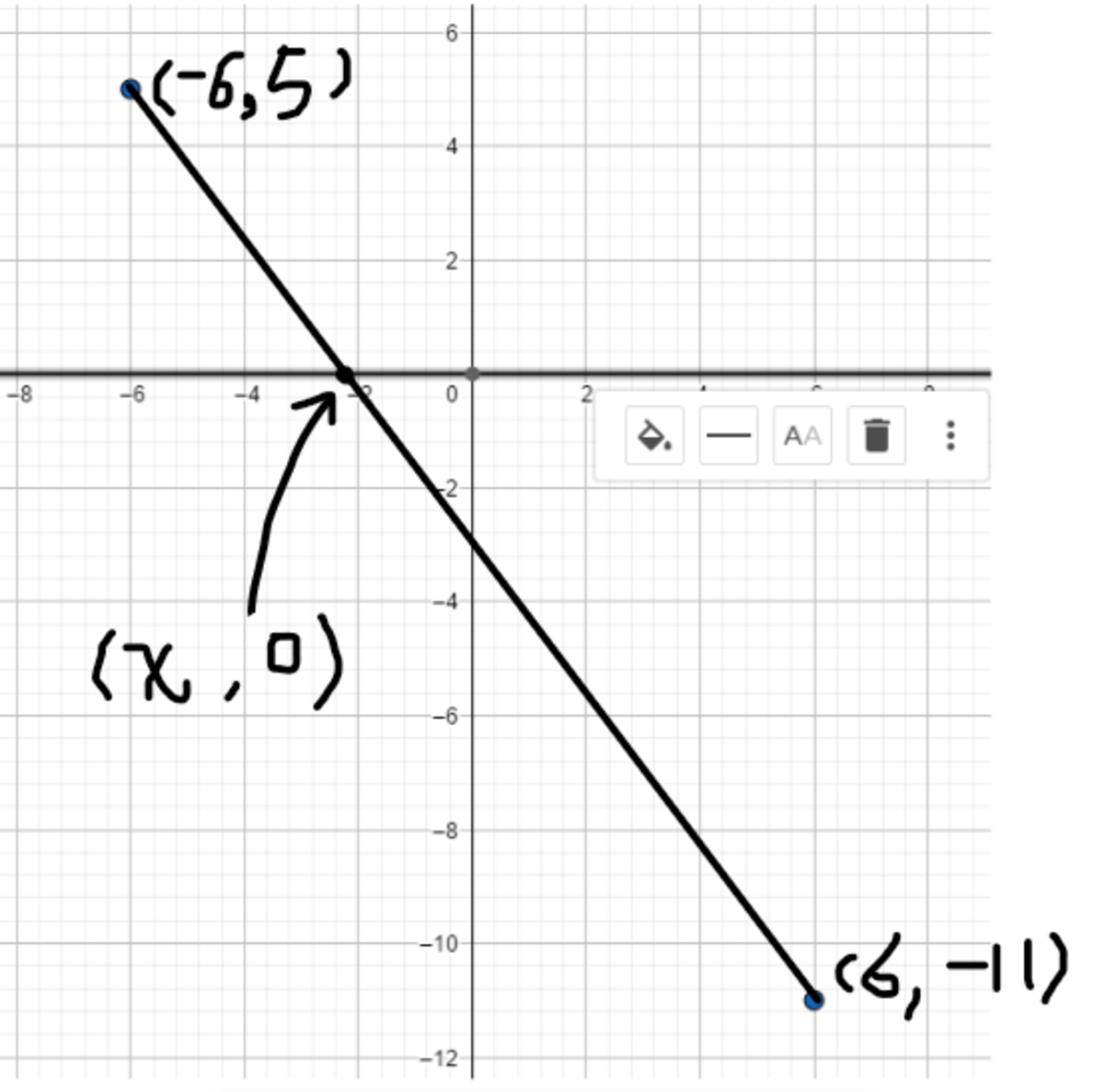 The distance between
(
−
6
,
5
)
and
(
x
,
0
)
is
2
(
x
−
(
−
6
)
)
2
+
(
5
−
0
)
2
=
2
(
x
+
6
)
2
+
2
5
. The distance between
(
x
,
0
)
and
(
6
,
−
1
1
)
is
2
(
x
−
6
)
2
+
(
0
−
(
−
1
1
)
)
2
=
2
(
x
−
6
)
2
+
1
2
1
. The minimum value of the original formula is the distance between two blue dots:
2
(
(
−
6
)
−
6
)
2
+
(
5
−
(
−
1
1
)
)
2
=
2
1
2
2
+
1
6
2
=
2
1
4
4
+
2
5
6
=
2
4
0
0
=
2
0
The distance between
(
−
6
,
5
)
and
(
x
,
0
)
is
2
(
x
−
(
−
6
)
)
2
+
(
5
−
0
)
2
=
2
(
x
+
6
)
2
+
2
5
. The distance between
(
x
,
0
)
and
(
6
,
−
1
1
)
is
2
(
x
−
6
)
2
+
(
0
−
(
−
1
1
)
)
2
=
2
(
x
−
6
)
2
+
1
2
1
. The minimum value of the original formula is the distance between two blue dots:
2
(
(
−
6
)
−
6
)
2
+
(
5
−
(
−
1
1
)
)
2
=
2
1
2
2
+
1
6
2
=
2
1
4
4
+
2
5
6
=
2
4
0
0
=
2
0
I used GeoGebra to draw the plane coordinate system. :)
Using the diagram by Dan Lawson A C = 1 2 2 + 1 6 2 = 2 0 .
The best way to solve this problem is using MatLab to graph the whole function from -100 to 100.
It isn't about getting the answer right, it is about sharping your problem solving skills.
Remember to increase finest.
I think the problem solving skills imply using all tools available, theoretical or otherwise, to find the answer. Besides that, to qualify as best, the solution must be evaluated along some desirable characteristic. Obviously, this solution cannot be classified as elegant in mathematical terms, but If the characteristic is time, this could be a very good solution with low error margin. On the other hand, If evaluated in relation to computing resources, using the Android Mathematics app to generate the graph is better, considering availability and total cost of hardware/software.
a lot of people have brilliant solutions and i am here hacking the system graphed it on desmos and figured it out
The derivative is 0 at x=-2.25. The value at this point is 20 and a bigger value can easily be found to show that it is minima.
Can someone help me to understand what's wrong in the following solutions?
Since the two member of the expression represent triangles i tried to use the triangular inequality. If you do all the calculations you get x<-6 and x<6. The two equations must be true at the same time, so x < -6 is the solution. If you substitute for x = -6 you get 21.2something. Round up to 22 or down to 21 doesn't work. Why?
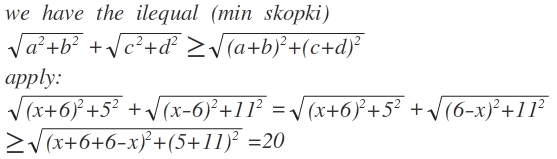

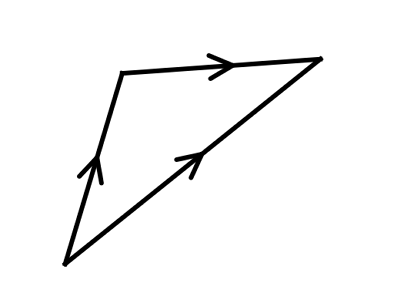
Consider the figure below. Title of picture
A
B
=
(
x
+
6
)
2
+
2
5
and
B
C
=
(
x
−
6
)
2
+
1
2
1
.
The sum
A
B
+
B
C
is minimized when
x
is such that
A
B
+
B
C
=
A
C
=
2
0
.
Title of picture
A
B
=
(
x
+
6
)
2
+
2
5
and
B
C
=
(
x
−
6
)
2
+
1
2
1
.
The sum
A
B
+
B
C
is minimized when
x
is such that
A
B
+
B
C
=
A
C
=
2
0
.