The miraculous integer
× A A 8 A A 0 A A 0 A A 1
What is the three digit number A A A ?
The answer is 999.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Moderator note:
Yes correct. This works too.
hmmmm... nice
I did it exactly in the same way,its the best solution
I used trial and error
Why is this problem in level 3?
To rewrite the equation, we have:
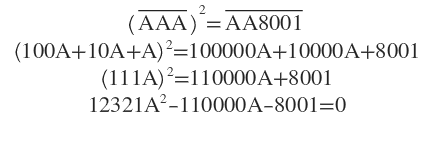
Then using the quadratic equation, we get:

Since subtracting it will lead us to a negative number, we just use addition. Hence,
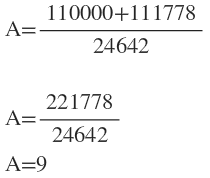
Therefore,
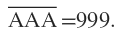 .
.
Moderator note:
That's some large calculation you got there. You could have simplified your work with Rational Root Theorem . Despite what I've said, there's a much simpler approach. Can you find it?
wow your terrible
Even if you do not recognize the last four digits, shown undisguised, as being those of 998,001 = 999 x 999 (I did, in milliseconds) there are only two theoretically possible solutions given that the square njumber ends in 1 - 111 and 999 and it does not take long to establish that 111 is wrong (or indeed if you start high that 999 is right).
1 2 3 2 1 A 2 − 1 1 0 0 0 0 A − 8 0 0 1 can be factored.
Best solution............
The sum of the digits of A A A is 3 × A , so it's clearly divisible by 3 . The product A A A × A A A will therefor have to be divisible by 9 .
A + A + 1 + 8 must be a multiple of 9 , so 2 × A has to be a multiple of 9 . This is only posible if A = 9 .
As the last digit of the square of the given 3-digit number ends in 1 so we can conclude that either A=1 or 9 . We can easily predict that 111 x 111 is a 5-digit number. So, we get A=9, giving us the 3-digit number = 999
Moderator note:
Great work for knowing that 1 1 1 2 is a five digit number.
999 999=998001 Because 999=1000-1 So 999 999=(1000-1)(1000-1) Turn the former (1000-1) to A. Then A(1000-1) So 1000A-A. 1000(1000-1)-(1000-1) 1000000-1000-1000+1=990000-1000+1=980000+1=998001
Moderator note:
Please refrain from posting a solution that doesn't show any relevant working.
9^2=81 99^2=9801 999^2=998001 9999^2=99980001
The solution can be acquired by knowing this property of n digits of 9 being squared.
Moderator note:
This solution is too convenient. It's like saying that I know 9 9 9 2 = 9 9 8 0 0 1 beforehand so there's nothing to show.
hahahahaha
For the last digit of a perfect square to be 1 , A is either 1 or 9 , 1 1 1 2 = 1 2 3 2 1 = 1 1 8 0 0 1 , therefore the number must be 9 9 9 and 9 9 9 2 = 9 9 8 0 0 1 .