Geometrically Algebraic

The given triangle whose vertices are (0,0), (2,0) and (1,√3) of side length 2 is equilateral and thus its Fermat point is its centre which is at 2/√3 from each vertex. The required sum is therefore 3*2/√3 or 2√3.

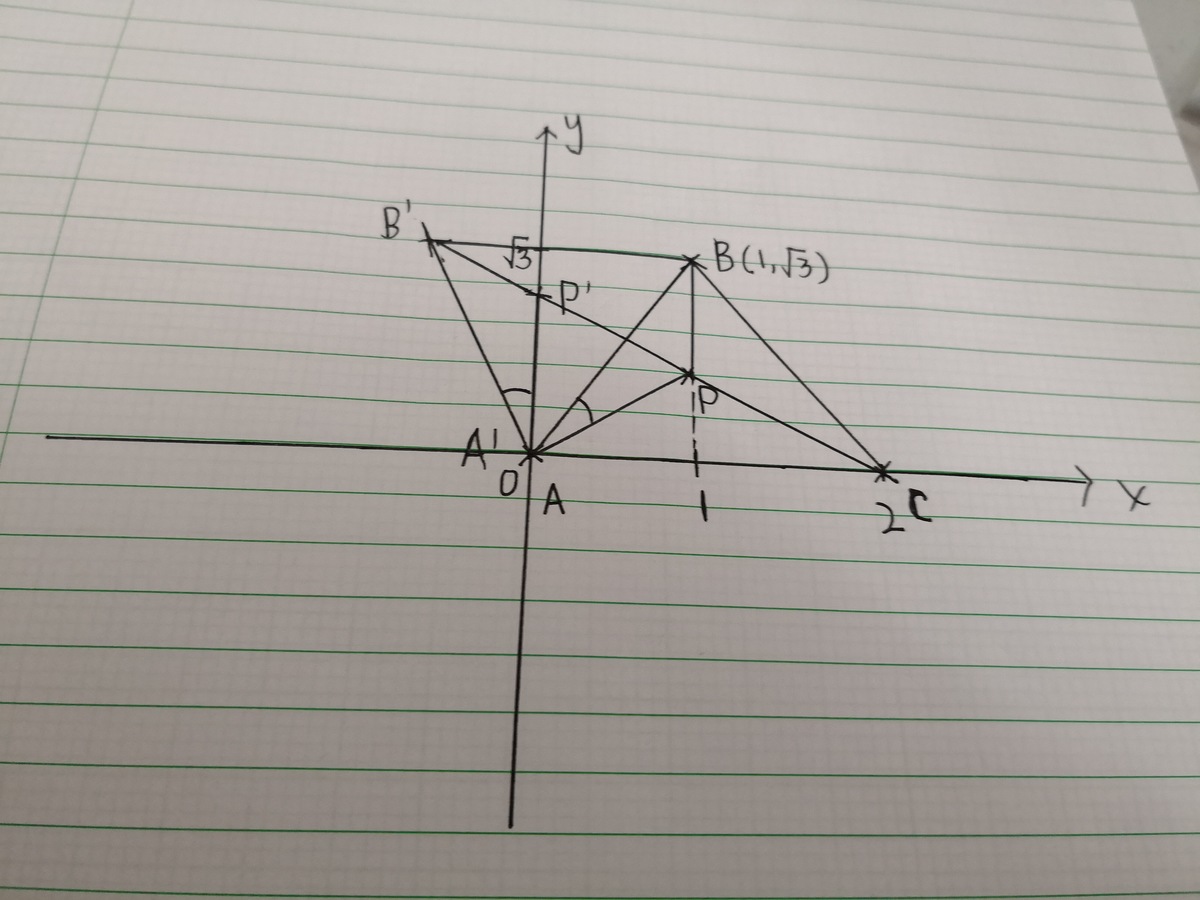
Let $A(0,0), B(1,\sqrt{3}), C(2,0), P(x,y)$

$f(x,y)=\sqrt{(x-2)^{2}+y^{2}}+\sqrt{x^{2}+y^{2}}+\sqrt{(x-1)^{2}+(y-\sqrt{3})^{2}}$

$|PA|+|PB|+|PC|=\sqrt{(x-2)^{2}+y^{2}}+\sqrt{x^{2}+y^{2}}+\sqrt{(x-1)^{2}+(y-\sqrt{3})^{2}}$

So, $f(x,y)=\sqrt{(x-2)^{2}+y^{2}}+\sqrt{x^{2}+y^{2}}+\sqrt{(x-1)^{2}+(y-\sqrt{3})^{2}}$

Now, rotate $\Delta PAB$ in $60^\circ{}$ anticlockwise about point $A$ and construct the triangle $\Delta BB^{'}A$ .

Let the image of point $A$ be $A^{'}$ , the image of point $B$ be $B^{'}$ , the image of point $P$ be $P^{'}$

$\Delta PAB\cong \Delta P^{'}A^{'}B^{'}$

$\angle P^{'} A^{'} B^{'}=\angle PAB$

Let $\angle P^{'} A^{'} B^{'}=\angle PAB=\theta$

$\angle P^{'} A^{'} B=60^\circ{}-\theta$

$\angle P^{'} A^{'} B+\angle PAB=60^\circ{}-\theta+\theta=60^\circ{}$

$\angle PA^{'}P^{'}=60^\circ{}$

and $|PA|=|P^{'}A^{'}|$ with point $A$ coinciding with point $A^{'}$

So, $\Delta PAP^{'}$ is an equilateral triangle.

$|P^{'}P|=|P^{'}A|=|PA|$

Since $\Delta PAB\cong \Delta P^{'}A^{'}B^{'}$ ,

Then, $|P^{'}B^{'}|=|PB|$

Therefore $|PA|+|PB|+|PC|=|P^{'}P|+|P^{'}B^{'}|+|PC|$

When points $B^{'},P^{'},P,C$ are collinear,

$|P^{'}P|+|P^{'}B^{'}|+|PC|=|B^{'}C|$

$|P^{'}P|+|P^{'}B^{'}|+|PC|$ is minimum.

$A^{'}B^{'}=AC=2, \angle B^{'}A^{'}C=60^\circ{}\times 2=120^\circ{}$

$|B^{'}C|^{2}=2^{2}+2^{2}-2(2)(2)\cos120^\circ{}$

$|B^{'}C|^{2}=4+4+-8(\cfrac{-1}{2})$

$|B^{'}C|^{2}=12$

$|B^{'}C|=2\sqrt{3}$

Minimum value of $|P^{'}P|+|P^{'}B^{'}|+|PC|=2\sqrt{3}$

Hence, minimum value of $f(x,y)=2\sqrt{3}$

$a+b=2+3=5$

See also, Fermat's Point