The Mississippi Problem
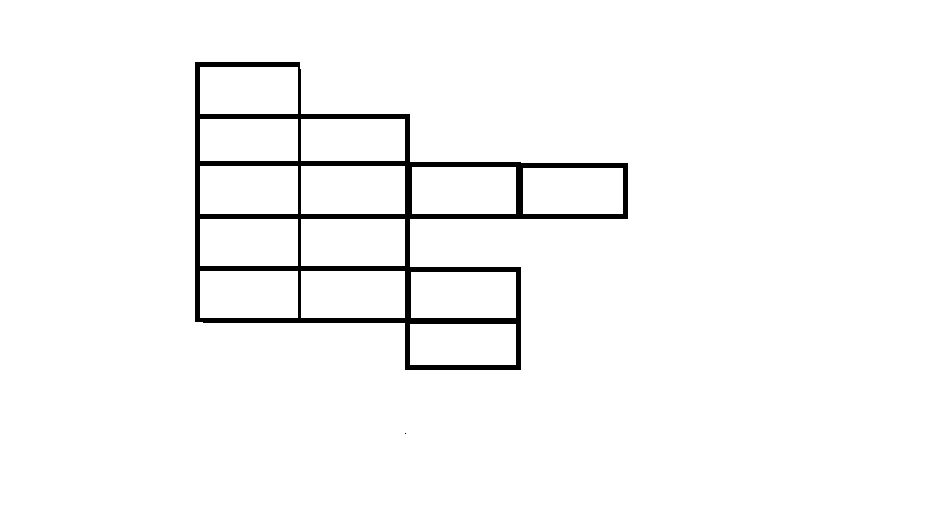
Find the number of different ways in which the letters of the word MISSISSIPPI can be placed in the 13 given boxes such that no row remains empty .
This question is posed by Rajat Bhagat .
You can try more of my Questions here .
The answer is 1836450.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Frst, we choose which 11 of the 13 boxes to fill with letters. This is equivalent to choosing two squares to be empty.
Label the rows A, B, C, D, E, F, from top to bottom. The two empty boxes are either in the same row, or they are in different rows. If they are in the same row, it must be row C or row E. There are ( 2 4 ) = 6 ways to choose two squares from row C, and ( 2 3 ) = 3 ways to choose two squares from row E.
Otherwise, the two empty squares are in different rows. We choose two rows from rows B, C, D, E, and then we choose a square from each row. This leads to 2 ⋅ 4 + 2 ⋅ 2 + 2 ⋅ 3 + 4 ⋅ 2 + 4 ⋅ 3 + 2 ⋅ 3 = 4 4 possibilities.
So there are 6 + 3 + 4 4 = 5 3 ways to choose two squares to be empty, so 53 ways to choose which 11 of the 13 boxes to fill. There are then 4 ! 4 ! 2 ! 1 1 = 3 4 6 5 0 ways to arrange the letters of MISSISSIPPI, for a total of 5 3 ⋅ 3 4 6 5 0 = 1 8 3 6 4 5 0 ways.
This is solution provided by sir Jon Haussman .
Actually there's a better way to get 53 ways. We need to find two empty space in the 11 spaces of the 4 rows in the middle. But those two space couldn't appear together in the second or the fourth row, therefore we have to minus 2 from the final result. So that's: 11C2 - 2= 53