The more the merrier ....
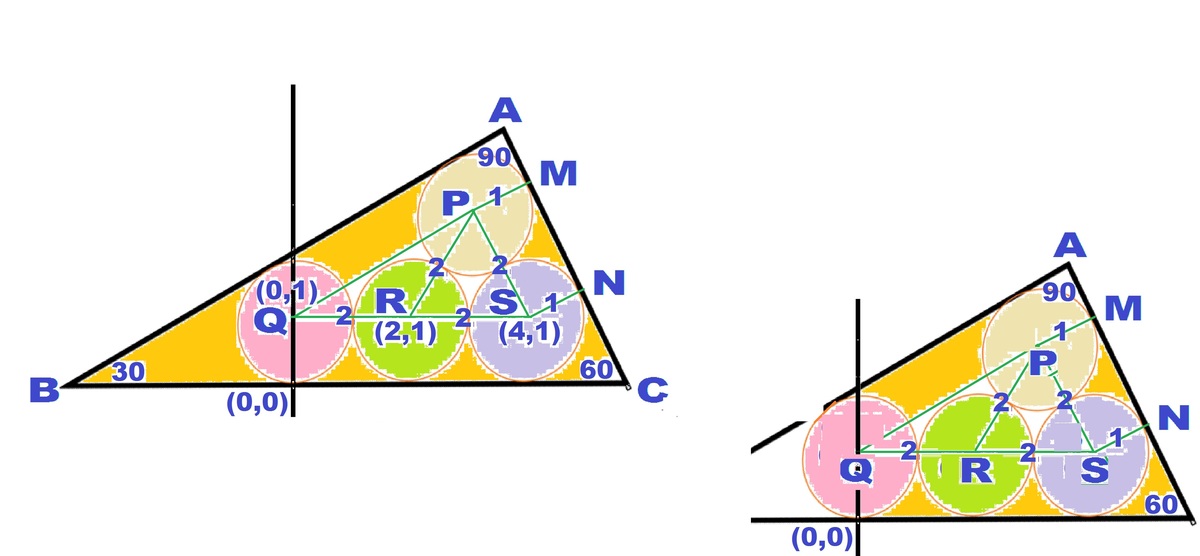
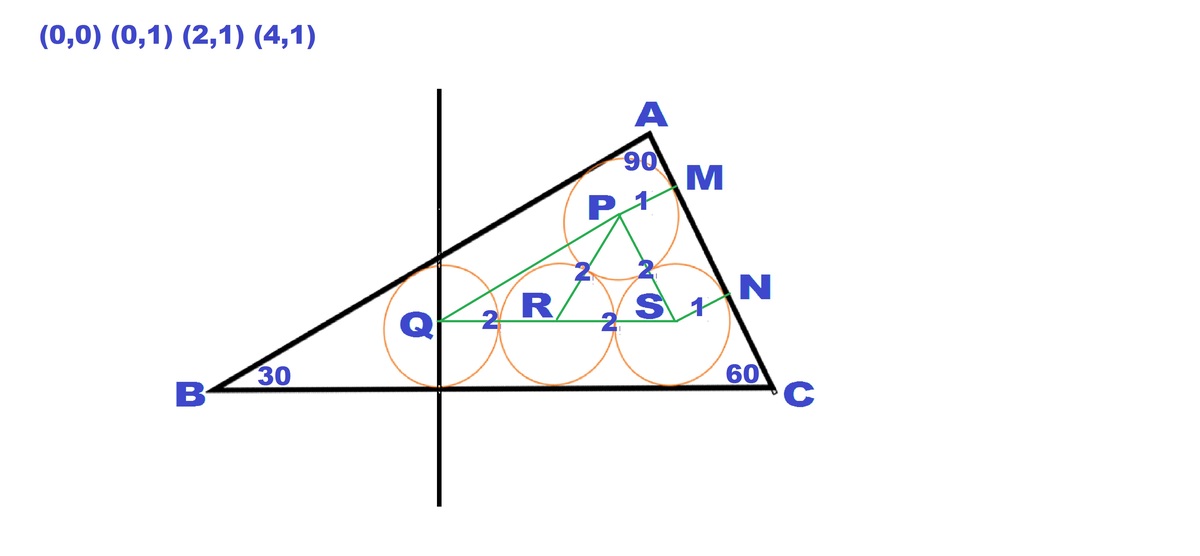
Suppose we have 4 circles P , Q , R , S each of radius 1 such that Q is centered at ( 0 , 1 ) , R at ( 2 , 1 ) , S at ( 4 , 1 ) and with P lying in the first quadrant tangent to both R and S .
Form a triangle Δ A B C that circumscribes the 4 circles such that A B is tangent to P and Q , A C is tangent to P and S , and B C is tangent to Q , R and S .
The perimeter of Δ A B C can be written as a + b c , where a , b , c are positive integers with c being square-free. Find a + b + c .
The answer is 21.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
 P
R
S
i
s
a
2
−
2
−
2
Δ
.
S
i
n
c
e
R
a
n
d
S
a
r
e
g
i
v
e
n
,
P
(
3
,
1
+
3
)
.
Let M and N be the points of tangency. So MPSN is a rectangle. Implies MN=PS=2
A
C
∣
∣
P
S
∴
s
l
o
p
e
o
f
A
C
=
−
3
.
⟹
B
C
A
=
6
0
o
.
A
B
∣
∣
P
Q
∴
s
l
o
p
e
o
f
A
B
=
3
3
.
⟹
A
B
C
=
3
0
o
.
⟹
A
B
C
i
s
a
r
t
.
∠
e
d
Δ
,
r
t
.
∠
e
d
a
t
A
.
∴
T
a
n
g
e
n
t
l
e
n
g
t
h
f
r
o
m
A
M
=
1
∵
i
t
i
s
a
s
i
d
e
o
f
a
s
q
u
a
r
e
.
.
T
a
n
g
e
n
t
l
e
n
g
t
h
f
r
o
m
C
=
C
o
t
2
6
0
1
=
3
.
S
o
A
C
=
A
M
+
M
N
+
N
C
=
1
+
2
+
3
=
3
+
3
.
P
e
r
i
m
e
t
e
r
o
f
3
0
−
6
0
−
9
0
Δ
A
B
C
=
(
1
+
3
+
2
)
∗
A
C
=
(
3
+
3
)
2
=
1
2
+
6
∗
3
.
a
+
b
+
c
=
2
1
P
R
S
i
s
a
2
−
2
−
2
Δ
.
S
i
n
c
e
R
a
n
d
S
a
r
e
g
i
v
e
n
,
P
(
3
,
1
+
3
)
.
Let M and N be the points of tangency. So MPSN is a rectangle. Implies MN=PS=2
A
C
∣
∣
P
S
∴
s
l
o
p
e
o
f
A
C
=
−
3
.
⟹
B
C
A
=
6
0
o
.
A
B
∣
∣
P
Q
∴
s
l
o
p
e
o
f
A
B
=
3
3
.
⟹
A
B
C
=
3
0
o
.
⟹
A
B
C
i
s
a
r
t
.
∠
e
d
Δ
,
r
t
.
∠
e
d
a
t
A
.
∴
T
a
n
g
e
n
t
l
e
n
g
t
h
f
r
o
m
A
M
=
1
∵
i
t
i
s
a
s
i
d
e
o
f
a
s
q
u
a
r
e
.
.
T
a
n
g
e
n
t
l
e
n
g
t
h
f
r
o
m
C
=
C
o
t
2
6
0
1
=
3
.
S
o
A
C
=
A
M
+
M
N
+
N
C
=
1
+
2
+
3
=
3
+
3
.
P
e
r
i
m
e
t
e
r
o
f
3
0
−
6
0
−
9
0
Δ
A
B
C
=
(
1
+
3
+
2
)
∗
A
C
=
(
3
+
3
)
2
=
1
2
+
6
∗
3
.
a
+
b
+
c
=
2
1
Nice solution with great graphics. Thanks for posting it. :)
Letting P , Q , R , S represent the centers of the respective circles, we have that Δ P R S is equilateral with side lengths 2 . Now Δ P R Q is isosceles with ∠ P R Q = 1 2 0 ∘ , and so ∠ P Q R = 3 0 ∘ . Thus Δ P Q S is a 3 0 / 6 0 / 9 0 right triangle with side lengths P S = 2 , Q S = 4 and P Q = 2 3 , giving us a perimeter for Δ P Q S of 6 + 2 3 .
Now as the 4 circles have the same radius we can conclude that Δ A B C is a 3 0 / 6 0 / 9 0 triangle as well. So if we can find the ratio of A B to P S we can multiply this ratio by the perimeter of Δ P Q S to get the perimeter of Δ A B C .
Now draw perpendiculars from P and S to A B intersecting at the respective points M , N . Then since ∠ P A M = 4 5 ∘ and ∠ S C N = 3 0 ∘ we have that
A B = A M + M N + N C = 1 + 2 + 3 = 3 + 3 .
The perimeter of Δ A B C is then
2 ( 3 + 3 ) ∗ ( 6 + 2 3 ) = 1 2 + 6 3 , and so
a + b + c = 1 2 + 6 + 3 = 2 1 .