The Most and the Least of Mickey
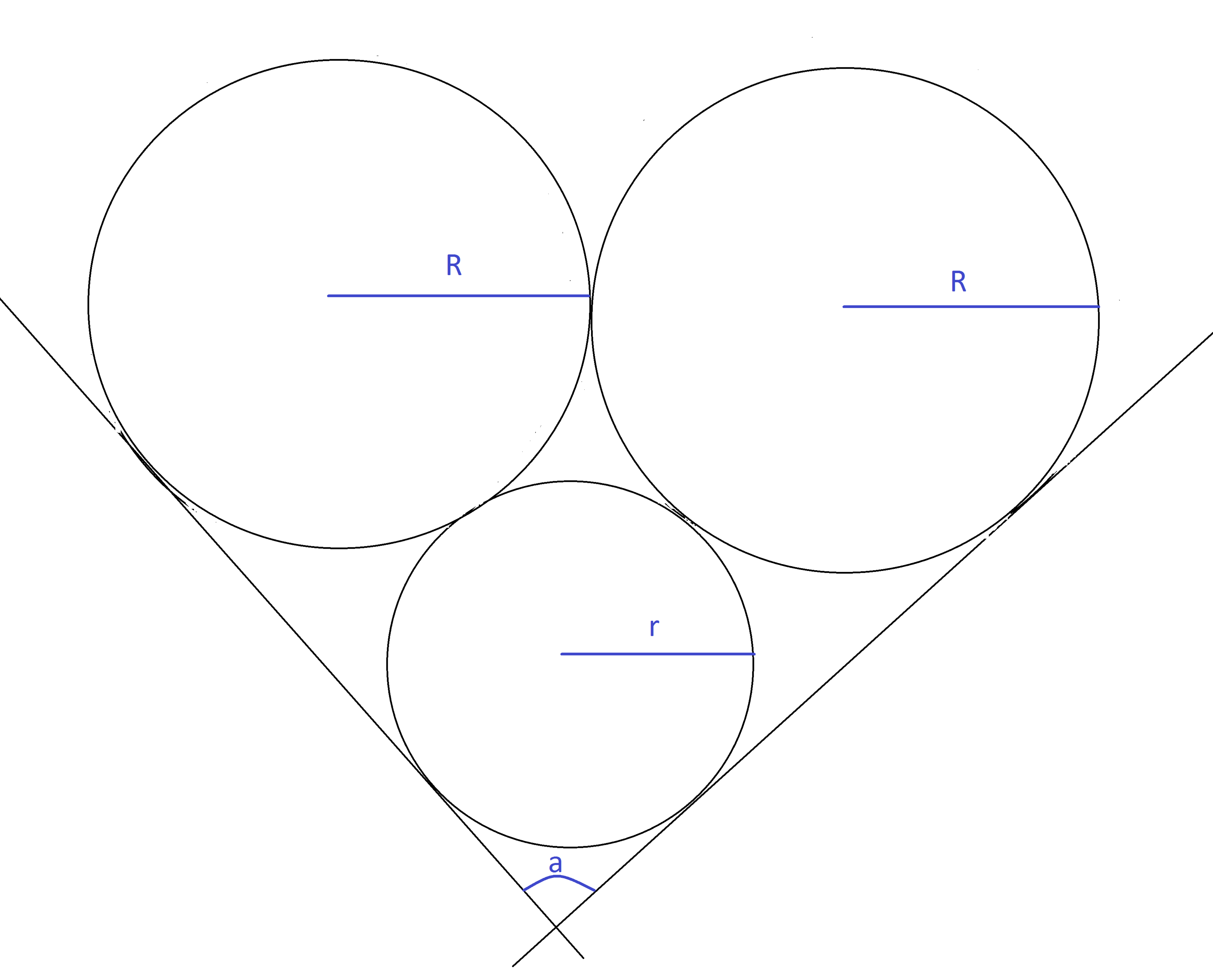
Two lines intersect each other forming an angle . A circle of radius is tangent to both of these lines. Two equal size circles with radius are:
(1)
: tangent to this circle,
(2)
: tangent to each other at a point more distant from the intersection of the lines than the center of the original circle, and
(3)
: each tangent to one of the lines,
As the size of the angle changes, so does the value of the ratio . If and are the infimum and the supremum of the ratio respectively, report .
The answer is 4.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The ratio R / r is an increasing function of angle a which varies from near zero to almost 180 degrees. As angle a approaches zero, the two lines are close to parallel and the circles approach situation pictured below: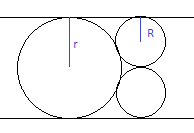
The limit of the ratio R / r for parallel lines, that is m , is then 2 1
At the other extreme as angle a approaches 180 degrees, situation is pictured below: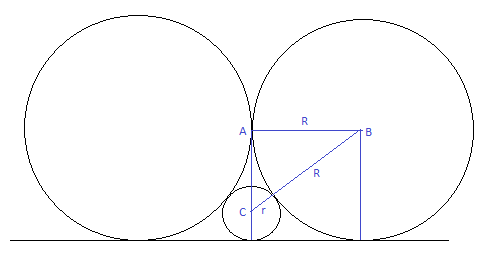
Sides of the right triangle ABC are R , R + r , and R − r . The ratio R / r can be calculated from the Pythagorean Theorem and comes to M = 4 . So M + m = 4 . 5 .