The moving snail problem
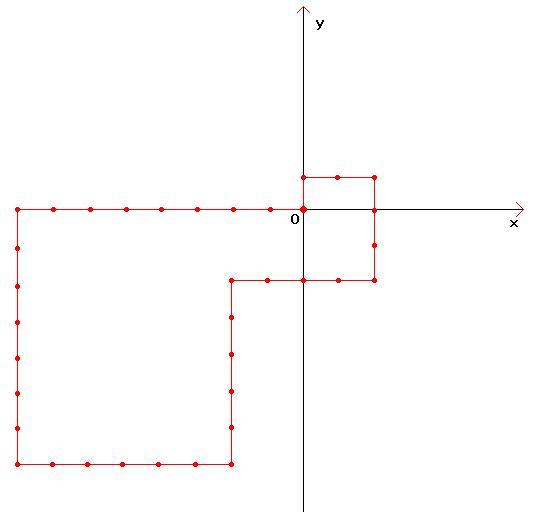
A snail moves on the ground, starting at its home at 9:00 A.M. It moves 1m during the first hour, 2m during the second hour, 3m during the third hour, and so on. At the end of each hour, it turns 90 degrees to the right or the left. Suppose the minimum distance between the snail and its home at 5:00 P.M, in meters, is a. Calculate ?
The answer is 0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
On the coordinate plane Oxy, suppose the house of the snail is at the point O and the snail moves from point O to point (0; 1) during the first hour. Since the snail turns 90 degrees to the left or to the right at the end of each hour and it moves vertically during the first hour, it also moves vertically during the third, fifth and seventh hour. Likewise, it moves horizontally during the remaining hours. To reduce the value of a most efficiently, both the x-coordinate and the y-coordinate must have the smallest possible value. Realizing that 1 − 3 − 5 + 7 = 0 and 2 − 4 − 6 + 8 = 0 , the snail can reach point O after 8 hours. Therefore, the minimum value of a 2 is 0. The image below shows one of the ways that the snail can move such that a 2 =0.