The Mysterious Brilliant Logo

Geometry Level 5

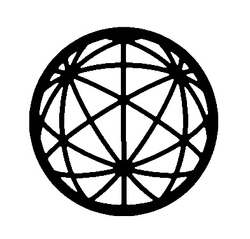If we think of the Brilliant logo \boldsymbol {\text {Brilliant logo}} in three dimensions as a sphere, what will be the total number of great circles there?


The answer is 15.

Md Omur Faruque by MD Omur Faruque , 25, Bangladesh

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

Md Omur Faruque
Aug 5, 2015

B r o w n \color{#624F41}{Brown} , C y a n \color{cyan}{Cyan} , M a g e n t a \color{magenta} {Magenta} , Y e l l o w \color{#CEBB00} {Yellow} and G r e e n \color{#20A900} {Green} , 3 great circles from each color making a total of 15 \color{#69047E} {\boxed{15}} .

17 Helpful 0 Interesting 0 Brilliant 0 Confused

Julian Poon - 5 years, 10 months ago

Log in to reply

Do these have a name?

Ryan Tamburrino - 5 years, 10 months ago

Is this just a picture or it has some kind of meaning? Because, I'm not getting it.

MD Omur Faruque - 5 years, 10 months ago

Log in to reply

nah... its just a picture

Julian Poon - 5 years, 10 months ago

i think instead of this picture if you focus on 3 main junctions of original picture you can calculate the answer easily.

Gautam Aasundra - 5 years, 10 months ago

Log in to reply

yes, exactly!

Maria Quadeer - 5 years, 10 months ago

And, how is that? I can see each point is an intersection of five points, but then....?

MD Omur Faruque - 5 years, 10 months ago
Joel Toms
Aug 7, 2015

Consider the points where 5 circles intersect. These correspond to the centres of the faces of a regular dodecahedron. Each circle passes through 4 such points, so:

No. of circles = No. of points where 5 circles meet × No. of circles meeting at each point No. of such points each circle passes through = 12 × 5 4 = 15 . \textrm{No. of circles}=\frac{\textrm{No. of points where 5 circles meet}\times\textrm{No. of circles meeting at each point}}{\textrm{No. of such points each circle passes through}}=\frac{12\times5}4=\boxed{15\,}.

12 Helpful 0 Interesting 0 Brilliant 0 Confused

Nice solution. But finding the number of intersection points (which is 12 indeed) isn't much easier than finding the number of circles.

MD Omur Faruque - 5 years, 10 months ago

Log in to reply

If you notice the pentagonal pattern that these points make, it is natural to conclude that the same continues around the sphere. It made sense in my head anyway. Plus, I built a model out of Geomag just to be sure X-)

Joel Toms - 5 years, 10 months ago
Ikoz Manzukovski
Jun 24, 2018

There is a problem that outright visually portrays the 15 circles of the logo in its set-up, I instantly answered this just by having seen that problem.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...