The Mystic Triangle
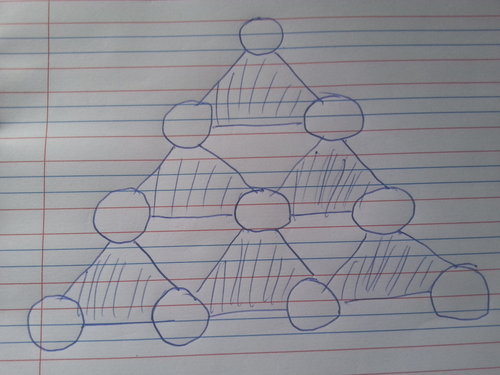 Insert the digits 0 to 9 without repetition in the 10 circles at the vertices of the figure above such that the sum of the numbers in the vertices of each shaded triangle is equal.
Insert the digits 0 to 9 without repetition in the 10 circles at the vertices of the figure above such that the sum of the numbers in the vertices of each shaded triangle is equal.
Among the solutions that exist, the vertex in the Center circle can have only certain possible values. Find the product of those possible values.
The answer is 18.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Great problem and great solution, Satyen! I used similar arguments, except for one little shortcut based on symmetry: If you have a solution, you get another one by replacing all your numbers x by 9 − x . Thus it suffices to consider center values ≤ 4 , eliminating the need for your cases (C) and (D).
It seems like there is only one way to place the numbers 0,..,9, up to symmetry (rotation, reflection, and x vs 9 − x symmetry).
Log in to reply
Tx Otto. Good point !
Haha, I used the same shortcut too, so I knew definitely that the answer was either 18 or 0!
Case B and C are not complete; you need to show that both of them can actually exist. Writing only which numbers go to corners and such isn't enough to show that the examples can actually exist.
Log in to reply
Thanks Ivan.. have put in two possible solutions
Here is a minizinc model to solve this with a legendary solver
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
|
Run with
./mzn-g12fd --all-solutions /tmp/mystic.mzn
Refer to my (in progress) wiki on discrete probability distribution - uniform distribution , to know what this means
Let x , y , z , T be the center value, the sum of the hexagon ring, the sum of the triangle corners, and the mutual triangle sum, respectively.
Note the following relationships:
0 + 1 + ⋯ + 4 + 5 = 1 5 ≤ y ≤ 3 9 = 4 + 5 + ⋯ + 8 + 9
3 x + 2 y + z = 6 T and 3 x + y = 3 T imply that z = 3 x
x + y + z = 4 5 then implies that 4 x + y = 4 5
From the equations above, derive that x ≡ y ≡ z ≡ 0 m o d 3 and y ≡ 1 m o d 4 .
Therefore, the possibilities for x , y , z are 6 , 2 1 , 1 8 and 3 , 3 3 , 9 , respectively. A quick check indicates that both are indeed possible.
It is easy to see that total (T) of all numbers of vertices of the graph is divisible by 6. But this total in the range [65..96]. Try some values: 66, 72, 78, 84, 90, 96. But this total minus total of number of the range: [0..9] is: total of number of three inner triangles-number in the center C. T − 4 5 = 3 × 6 T − C = 2 T − C C = 4 5 − 2 T Try more conditions to get C=6 when T=78 or C=3 by T=84. R e s u l t = 1 8
The three corner triangle sums + center number = 4 5 . Since each triangle sum is equal and 4 5 is divisible by 3 , center number can only be 0 , 3 , 6 , 9
( A ) If center vertex is 0 the sum of each triangle is 1 5 . Now the middle three triangles that share the center number each must sum up to 1 5 . But we don't have three sets of 2 numbers to sum up to 1 5 in the middle triangles. Only ( 7 , 8 ) and ( 9 , 6 ) . So center vertex cant be 0 .
( B ) If center vertex is 3 , the sum of each triangle is 1 4 . The middle three triangles that share the center number can have three sets of two numbers that sum up to 1 1 viz ( 5 , 6 ) , ( 4 , 7 ) and ( 9 , 2 ) . So 3 can be center vertex. The numbers not used 0 , 1 , 8 , are our corner vertices.
( C ) If center vertex is 6 , the sum of each triangle is 1 3 . The middle three triangles that share the center number can have three sets of two numbers that sum up to 7 viz ( 0 , 7 ) , ( 2 , 5 ) and ( 3 , 4 ) . So 6 can be center vertex. The numbers not used 1 , 8 , 9 are our corner vertices.
( D ) If center vertex is 9 the sum of each triangle is 1 2 . Now the middle three triangles that share the center number each must sum up to 1 2 . But we don't have three sets of 2 numbers to sum up to 3 in the middle triangles. Only ( 0 , 3 ) and ( 2 , 1 ) . So center vertex cant be 9 .
Our answer is 1 8 .