The net gravitational pull!
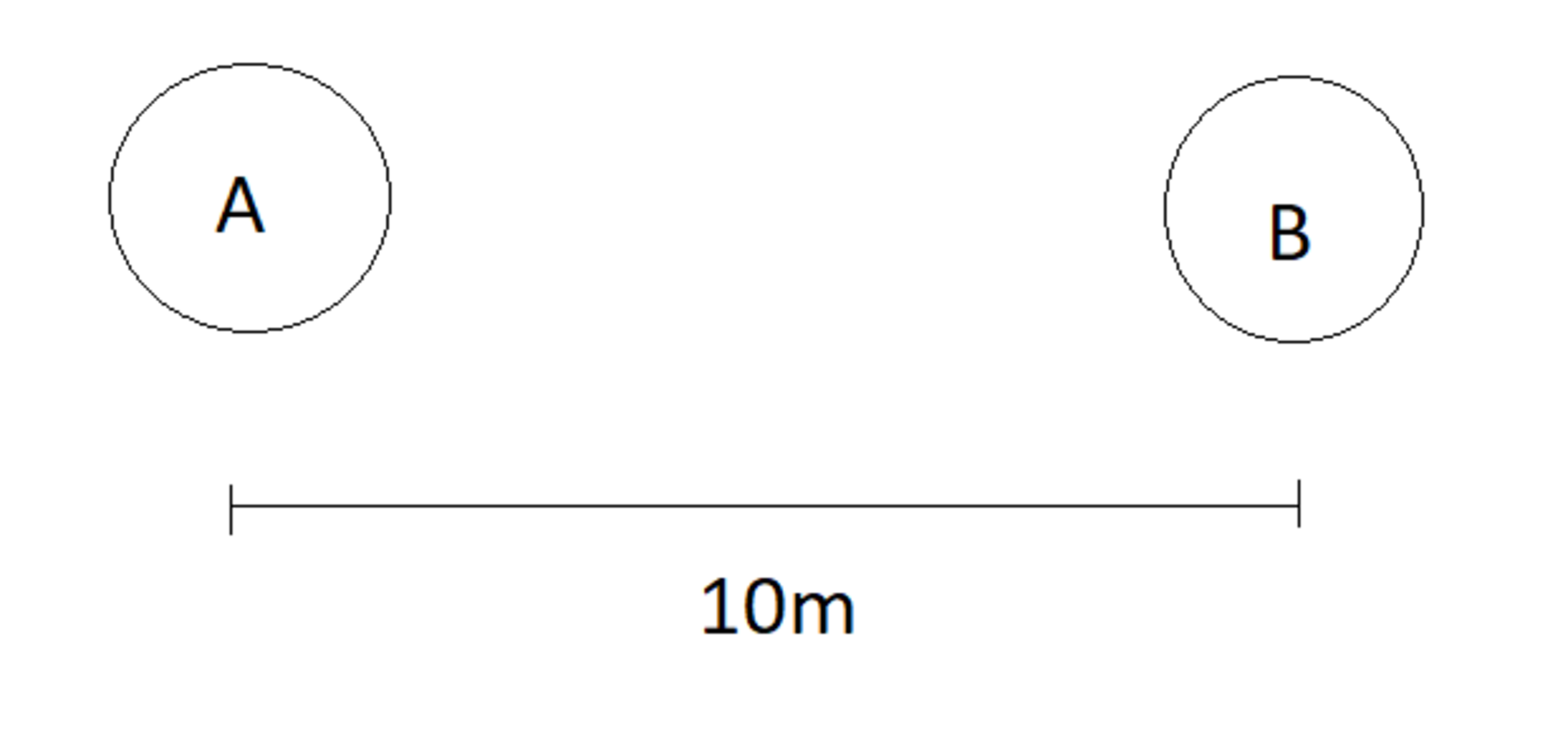
Two objects A and B are separated by a distance of 1 0 m (measured from there centers).
If ratio of there masses is 1 : 4 , then how far should be an object of mass 2 k g be placed from object A such that net gravitational force on it is 0 .
Note:
-
Assume that object B have larger mass than object A .
-
Submit answer till 2 digits after decimal point.
-
Submit answer in meters
The answer is 3.33.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Let the distance of the test mass m from the lighter body A be r m. Let the mass of A be M and that of B be 4 M .Then
r 2 G M m = ( 1 0 − r ) 2 4 G M m ⟹ 3 r 2 + 2 0 r − 1 0 0 = 0
⟹ r = 3 1 0 ≈ 3 . 3 3 3 m. Here G is the Universal Gravitational Constant.
It is not needed to make such a big quadratic equation and then solving it, it can be done in a more easier way! But after all it is a good solution.
Date of 2 Kg is not necesari .
Unic place to get g=0 is over the strait line that goes from A to B
Relation of Masses is 4 => relation of d^2 has to be too = 4 => relations of d = 2
d + 2d = 10 => d = 10/3 = 3.33....
Let the distance of the object of mass 2 k g from object A be x metres.
Let the mass of object A be m kilo-grams; therefore mass of object B is 4 m
=> It's distance from object B is 1 0 − x metres.
Let the force of gravitation acted on the object with mass 2 k g by object A be F A and by object B be F B
From newton's Universal law of gravitation we get F A = x 2 2 G m F B = ( 1 0 − x ) 2 2 G ( 4 m ) = ( 1 0 − x ) 2 8 G m
As F A and F B must be equal in magnitude x 2 2 G m = ( 1 0 − x ) 2 8 G m x 2 1 = ( 1 0 − x ) 2 4 4 x 2 = ( 1 0 − x ) 2 2 x = 1 0 − x 3 x = 1 0 x = 3 1 0 = 3 . 3 3 3 3 . . .