The nine-point-circle (Part II)

Geometry Level 5

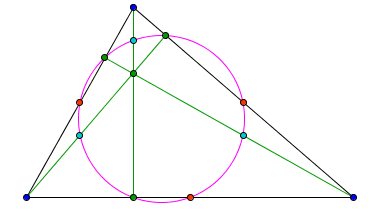
A circle pass through the following points in a triangle

The midpoint of each side.
The foot of each altitude.
The midpoint of the line segment from each vertex of the triangle to the orthocenter.

Find the perimeter of the triangle for which the radius of such circle is 10. Assume the triangle to have integer sides and area.

The answer is 96.

1 solution

Maria Kozlowska
Jan 4, 2016

When we look at the first Heronian triangle: $3 \times 4 \times 5$ we notice that the radius R of the circumcircle is $R=5/2 \Rightarrow R_{n} = R/2 = 5/4$ . For the radius of the nine point circle to be 10 we need to dilate our triangle by the ratio of 8, because: $5/4*8=10$

This gives us perimeter of $(3+4+5)*8=96$ .

Even I did it the same way,but can you prove that this is the only possible triangle under given conditions?

Indraneel Mukhopadhyaya - 5 years, 5 months ago

Searching the list of first primitive Heronian triangles does not give satisfactory result except the first one. $R_{n}=abc/(8 \triangle) \Rightarrow 80\triangle/(abc) =n$ , where n is integer only for the first triangle.

Maria Kozlowska - 5 years, 5 months ago

The nine-point-circle (Part II)

The answer is 96.

1 solution

0 pending reports