The nine-point-circle
For a triangle with sides 13, 15 and altitude 12, find the radius of the circle that passes through the following points:
- the midpoint of each side,
- the foot of each altitude, and
- the midpoint of the line segment from each vertex to the orthocenter.
If the radius can be written as a + n m , where a , m , and n are positive integers, m < n , and m and n are coprime, find a + m + n .
Note : Assume the given altitude to be through the vertex common to both the given sides.
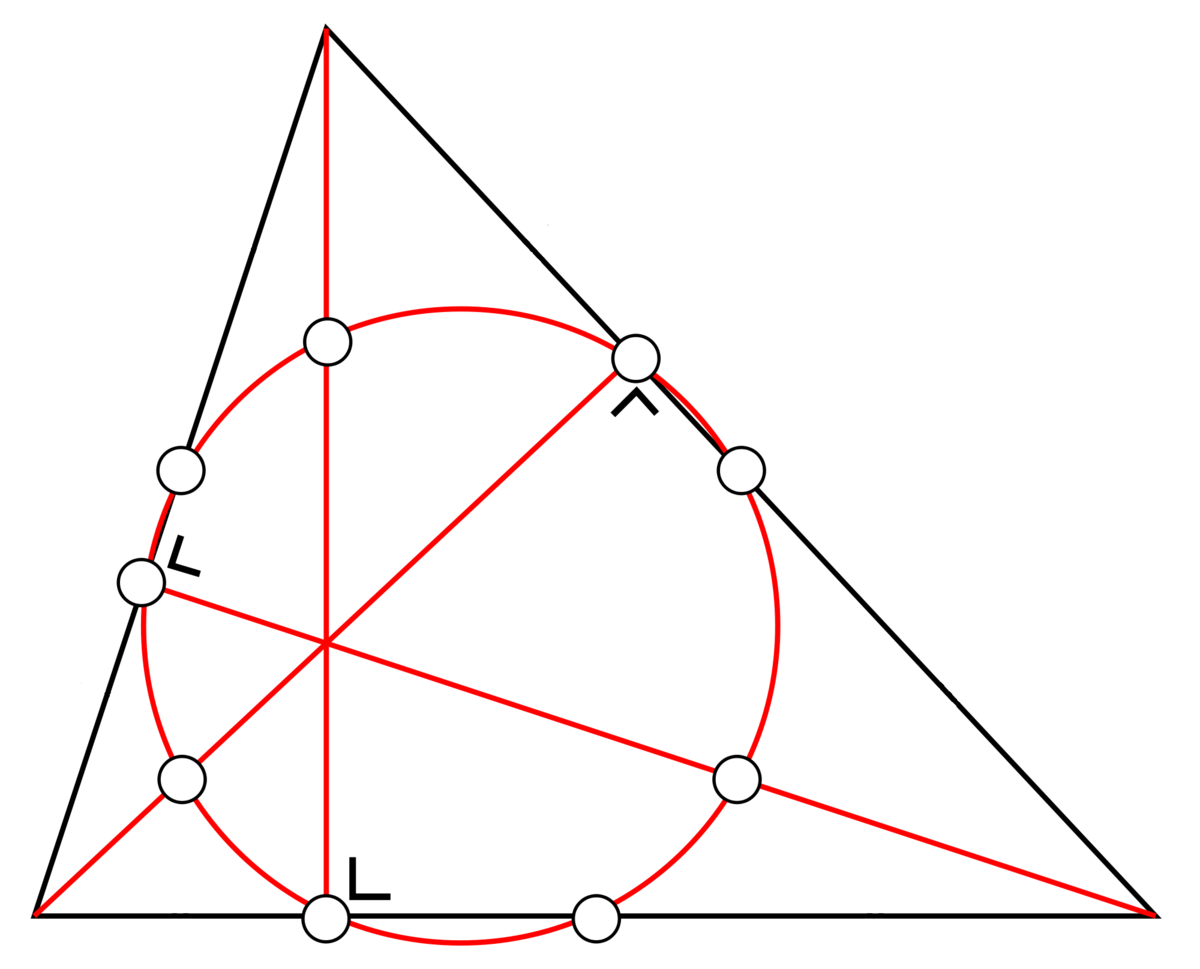
The answer is 21.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
If the altitude of length h lies between two sides of length a and b , and if the altitude divides the opposite side of the triangle into signed lengths x and y respectively, so that the third side of the triangle is c = x + y and a 2 = h 2 + x 2 and b 2 = h 2 + y 2 , then the sine of the angle of the triangle between the two sides a and b is (splitting the angle as the sum of the two angles formed by the altitude): sin C = a x × b h + a h × b y = a b h ( x + y ) = a b h c . Using the extended Sine Rule, the radius of the outcircle of the triangle is R = 2 sin C c = 2 h a b and so the radius of the nine-point circle is r = 2 1 R = 4 h a b .
Even without the rider that the altitude in question lies between the sides of length 1 3 and 1 5 , this question has a unique solution, since we are told that the radius of the nine-point circle is rational. While there are six possible triangles that have sides of 1 3 and 1 5 and with one altitude equal to 1 2 (two each for each of the three possibilities of where the altitude is in relation to the two known sides; in each case the altitude can meet the opposite side within the side itself, or else on the side extended), there are only two for which the nine-point circle has rational radius. These are the ones where (in my notation) a = 1 3 , b = 1 5 and h = 1 2 , in which case r = 1 6 6 5 = 4 1 6 1 .
I used co-ordinate geometry & a fact that:
"one and only one unique circle can pass through 3 given non-collinear points"
Let given triangle be ABC. AE is altitude from A meeting BC at E. AB is 13, AC is 15 and AE is 12. Hence BE is 5, EC is 9. Let D be midpoint of BC and F be midpoint of AC
Let BC become X-Axis and AE become Y-Axis, with origin at E(0,0). Hence A(0,12) ; B(-5,0) ; C(9,0) ; D(2,0) ; F(4.5,6) are the co-ordinates of various points.
Let equation of given circle be:
x²+y²+2gx+2fy+c=0
This passes through E(0,0), D(2,0) and F(4.5,6). Substituting the above co-ordinates we get:
c=0, g=-1, f=-63/16
The required radius being, r=√(g²+f²-c)=65/16
r=4+(1/16). Hence a+m+n=4+1+16=21
Note: we can verify that the above circle also passes through 6 other points by finding co-ordinate of all those points. I have used the easiest available co-ordinates for calculation, presuming that the answer is unique & question is correctly framed in a way that such a circle is actually possible with the given dimensions.
Continue to provide analytical geometry proof for problems. Very handy. I like it. Cheers!!!!!
Frankly speaking, I did not know much about nine-point circles. But, due to this question I Googled it and found out that if R is the circumradius of a triangle and R 0 is the radius of the nine point cirle.
Then they are related by the following formula,
R = 2 R 0
Now simply we can find out the third side of the triangle by the Pythagorean theorem, and it comes out to be 1 4 units.
Figuring out the are of the triangle( △ ),
△ = 0 . 5 ( 1 4 ) ( 1 2 )
△ = 8 4 square units.
Now we also know the relation,
4 △ a b c = R
Where a,b and c are the sides of the triangle.
Placing values,
4 ( 8 4 ) ( 1 3 ) ( 1 4 ) ( 1 5 ) = R
R = 8 6 5 units.
And,
R 0 = 1 6 6 5 units.
R 0 = 4 + 1 6 1 units.
Thanks for sharing this question, I learned a new thing out of it.