The number in the box is the number of times the number of the box occurs in the number
In the figure above , there are 10 boxes numbered 1 to 9. So you have to inscribe a 10 digit number such that the digit in the first box indicates the total number of 0's in the number , the digit in the box marked "1" indicates the total number of 1's in the number, and so on to the last box, whose digit indicates the total number of 9's in the number.Find this 10 digit number.
The answer is 6210001000.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Moderator note:
This is not a proper solution. Where is the relevant working?
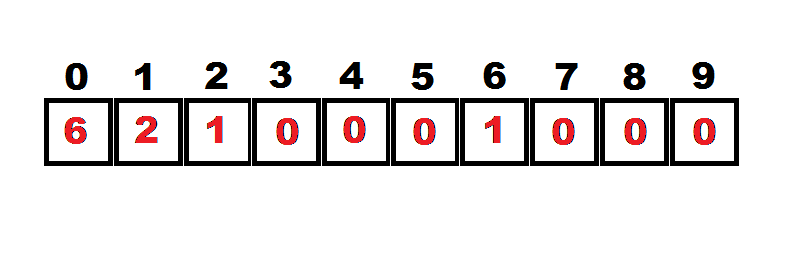
At first glance, there are at most 9 zeroes. If all 10 are zeroes, then even the zero place would be a zero which means there are zero 0's which results in a contradiction. Hence the number in the zero place MUST be a non-zero value.
But exactly how many zeroes should there be? This would determine the number that goes in the zero place. Assuming there are exactly x zeroes where x = 1, 2, 3...or 9. Then there would be an x in the zero place. But since we already have one x, there ought to be a 1 in the xth place. If there is a 1 in the nine place, then there would already be at least 1 one. Hence the number in the one place would be a non-zero value as well.
But if the number in the one place is 1, we face a contradiction as there is another place which also has a 1, resulting in at least 2 ones. So assume there are exactly 2 ones. This would give a 2 in the ones place. At the same time, we also have a 1 in the two place. Together with the 1 in the x place and the x in the zero place, we see that a total of 4 out of 10 places have already been occupied by non-zero values. So we have x+4 = 10 hence x=6. Therefore the number is 6210001000.