The odd theoretical ant
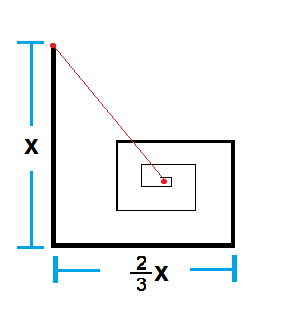 An ant travels along a straight path with a distance of
x
meters. From then on, it turns left and covers
3
2
of the straight distance it traveled before turning, and continues doing this until it eventually reaches an unknown point
P
(referred to as the red point in the middle of the picture). Refer to the figure above.
An ant travels along a straight path with a distance of
x
meters. From then on, it turns left and covers
3
2
of the straight distance it traveled before turning, and continues doing this until it eventually reaches an unknown point
P
(referred to as the red point in the middle of the picture). Refer to the figure above.
The distance of P from the ant's starting point is k x meters, where k is a positive constant which can be expressed in the form c a b , where g cd ( a , c ) = 1 and b is square free. Determine the value of a + b + c .
Challenge : Determine an explicit formula for k .
The answer is 29.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Nice problem but I could slove this one quite readily though :/
We embed the above picture in the coordinate system with the origin O , and assign the starting point the letter A . Its coordinates are 0 and x . To reach the apscise coordinate of P , we start from the point B ( 3 2 x , 0 ) , subtracting or adding distances alternatively. First, we subtract the next parallel distance to the segment O B , i.e. 3 2 x − ( 3 2 ) 3 x . In the next step, to this apscise we add ( 3 2 ) 5 x . Proceeding in the same way, we obtain 3 2 x − ( 3 2 ) 3 x + ( 3 2 ) 5 x − ⋯ + ( − 1 ) n − 1 ( 3 2 ) 2 n − 1 x + ⋯ = 1 3 6 x , and that is the apscise coordinate of P . Similarly, we obtain the ordinate coordinate of P , i.e. ( 3 2 ) 2 x − ( 3 2 ) 4 x + ( 3 2 ) 6 x − ⋯ + ( − 1 ) n − 1 ( 3 2 ) 2 n x + ⋯ = 1 3 4 x . So, the distance A P equals ( 1 3 6 x ) 2 + ( x − 1 3 4 x ) 2 = 1 3 3 x 1 3 , k = 1 3 3 1 3 . Here a = 3 , b = c = 1 3 , so a + b + c = 2 9 .
Let's assume that the ant starts from ( 0 , 0 ) .
Now let's say that the ant first moves distance x on x − a x i s .
The displacement of the ant on x − a x i s from ( 0 , 0 ) can be written as :
= x − 9 4 x + 8 1 1 6 x − … ∞
= 1 + 9 4 1 x = 1 3 9 x
Now let's say that the ant first moves distance 3 2 x on y − a x i s .
The displacement of the ant on y − a x i s from ( 0 , 0 ) can be written as :
= 3 2 x − 2 7 8 x + 2 4 3 3 2 − … ∞
= 1 + 9 4 3 2 x = 1 3 6 x
Now we just have to find the distance from ( 0 , 0 ) to ( 1 3 9 x , 1 3 6 x ) .
= ( 1 3 9 x − 0 ) 2 + ( 1 3 6 x − 0 ) 2
= 1 3 1 1 7 x = 1 3 3 1 3
⇒ k = 3 + 1 3 × 2 = 2 9
how you find displacement of the ant on x axis?
Wow I did the same........................................................
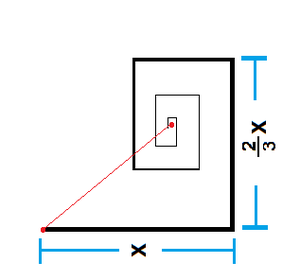
Turn the figure by 9 0 ∘ anticlockwise as shown above. Let the starting point be the origin of a complex plane and define the n th straight path as a complex number u n . We note that u n has a modulus of ( 3 2 ) n x and an argument of i n for non-negative integer n or u n = ( 3 2 i ) n x . Then the coordinates of the end of the n th straight path is given by ( ℜ ( z n ) , ℑ ( z n ) ) , where z n = ∑ k = 0 n u k and the distance from the starting point or origin is given by ∣ z n ∣ . Then, for n → ∞ , we have:
z ∞ ⟹ ∣ z ∞ ∣ = k = 0 ∑ ∞ ( 3 2 i ) n x = 1 − 3 2 i x = 3 − 2 i 3 x = 1 3 3 ( 3 + 2 i ) x = 1 3 3 1 3
Therefore a + b + c = 3 + 1 3 + 1 3 = 2 9 .
That's the best one I've ever seen
Is this complex bashing?
Log in to reply
Sort of complex bashing. And I like it. Upvote my solution if you like it.
The displacement on x axis is n = 0 ∑ ∞ x ( 3 2 ) 1 + 4 n − n = 0 ∑ ∞ x ( 3 2 ) 3 + 4 n and on y axis is n = 0 ∑ ∞ x ( 3 2 ) 2 + 4 n − n = 0 ∑ ∞ x ( 3 2 ) 4 n , so if the inital point is ( a . b ) , the final point, using geometric series, is ( a + 1 3 6 ⋅ x , b − 1 3 9 ⋅ x ) . Therefore, the distance between the inital point and the final point is 1 3 3 1 3
The distances travelled by the ant form a geometric progression. Let ( 0 , 0 ) be the starting point of the ant. Let r be the ratio of this geometric progression, which, in this case, is 3 2 .
The first turning point of the ant has coordinates ( 0 , − x ) . The second turning point has coordinates ( r x , − x ) . The third turning point has coordinates ( r x , − x + r 2 x ) . The fourth turning point has coordinates ( r x − r 3 x , − x + r 2 x )
and the pattern will go on such that P will have the coordinates of
( r x − r 3 x + r 5 x − r 7 x + . . . , − x + r 2 x − r 4 x + r 6 x + . . . ) .
So we can now simplify the coordinates of P, by determining the infinite geometric sums above, that is,
( 1 − r 4 ( r − r 3 ) x , 1 − r 4 ( − 1 + r 2 ) x ) ≡ ( x P , y P ) .
So the distance of P from the starting point is ( x P ) 2 + ( y P ) 2 . With some algebraic manipulation, we will find the distance to be equal to
d = 1 + r 2 x
Substituting for the values of d and r, thereby eliminating x, we find out that k = 1 3 3 1 3 . Thus the answer is 3 + 1 3 + 1 3 = 2 9 .