The ol' switcheroo function
 True or False:
True or False:
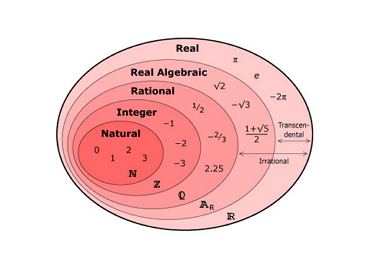
There exists a continuous function such that is rational whenever is irrational and irrational whenever is rational.
Image Credit: Flickr Congruent Triangles .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Suppose for the sake of contradiction such a function f exists. Since f ( x ) is sometimes rational and sometimes irrational, f isn't constant. So, there are values a < b such that f ( a ) = f ( b ) . Without loss of generality, suppose f ( a ) < f ( b ) . By the intermediate value theorem, for each irrational number y ∈ ( f ( a ) , f ( b ) ) , there exists an x ∈ ( a , b ) such that f ( x ) = y , where we know that x is rational by definition of f . Thus, f defines a surjection from the rational numbers in ( a , b ) to the irrational numbers in ( f ( a ) , f ( b ) ) , which is impossible since the former set is countable and the latter set is uncountable. So, no such function f exists.