The Overlapping Circles Problem
Let C 0 be a circle of radius 1 centred at the origin and C 1 be a circle of the same radius. Define f ( x ) as the area of the overlapping section between the two circles when C 1 is centred at ( x , 0 ) . The value of ∫ − 2 2 f ( x ) d x can be expressed as a fraction n m , where m , n ∈ Z + and g c d ( m , n ) = 1 . Find m n .
The answer is 4096.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
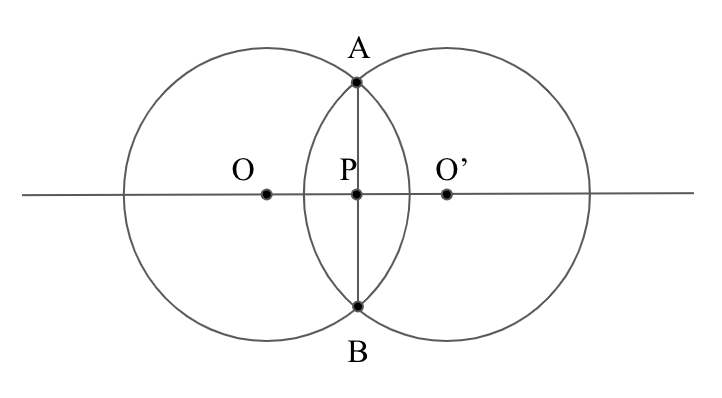 Consider the diagram above, where
O
denotes the centre of
C
0
and
O
’
denotes the centre of
C
1
. The area of the sector is equal to
(
sector
O
A
B
)
−
(
triangle
O
A
B
)
+
(
sector
O
’
A
B
)
−
(
triangle
O
’
A
B
)
.
Consider the diagram above, where
O
denotes the centre of
C
0
and
O
’
denotes the centre of
C
1
. The area of the sector is equal to
(
sector
O
A
B
)
−
(
triangle
O
A
B
)
+
(
sector
O
’
A
B
)
−
(
triangle
O
’
A
B
)
.
Length O P is equal to 2 x and since O A = 1 , A P = 1 − 4 x 2 . Angle A O P = a r c c o s ( 2 x ) and therefore angle A O B = 2 a r c c o s ( 2 x ) .
So sector O A B = a r c c o s ( 2 x ) and triangle O A B = 2 x 1 − 4 x 2 . The area of the overlapping section, f ( x ) , is twice the difference between the sector and the triangle and is therefore 2 a r c c o s ( 2 x ) − x 1 − 4 x 2 .
Integrate this expression from 0 to 2 to get 3 8 . So the integral from − 2 to 2 would be 3 1 6 as f ( x ) is symmetric across the y-axis. This yields m = 1 6 and n = 3 . m n = 1 6 3 = 4 0 9 6 , the desired result.
The overlapping section common to two circles is known as a lens . In this case, the area of the lens formed by C 0 and C 1 (when x ≥ 0 ) is
f ( x ) = π − 2 tan − 1 4 − x 2 x − 2 x 4 − x 2
or, slightly more conveniently,
f ( x ) = π − 2 sin − 1 2 x − 2 x 4 − x 2
Since 2 π − s i n − 1 2 x = c o s − 1 2 x , this is just
f ( x ) = 2 cos − 1 2 x − 2 x 4 − x 2
Note that this is only valid for x ≥ 0 (this is due to a signed area hidden in the last term). However, we clearly have f ( x ) = f ( − x ) , so we need to find
I = ∫ − 2 2 f ( x ) d x = 2 ∫ 0 2 f ( x ) d x = ∫ 0 2 [ 4 cos − 1 2 x − x 4 − x 2 ] d x
The integration tricks we need are integration of an inverse function (for the first term) and substitution (eg u = 4 − x 2 ) for the second term:
I = 8 − 3 8 = 3 1 6
leading to the answer 1 6 3 = 4 0 9 6 .