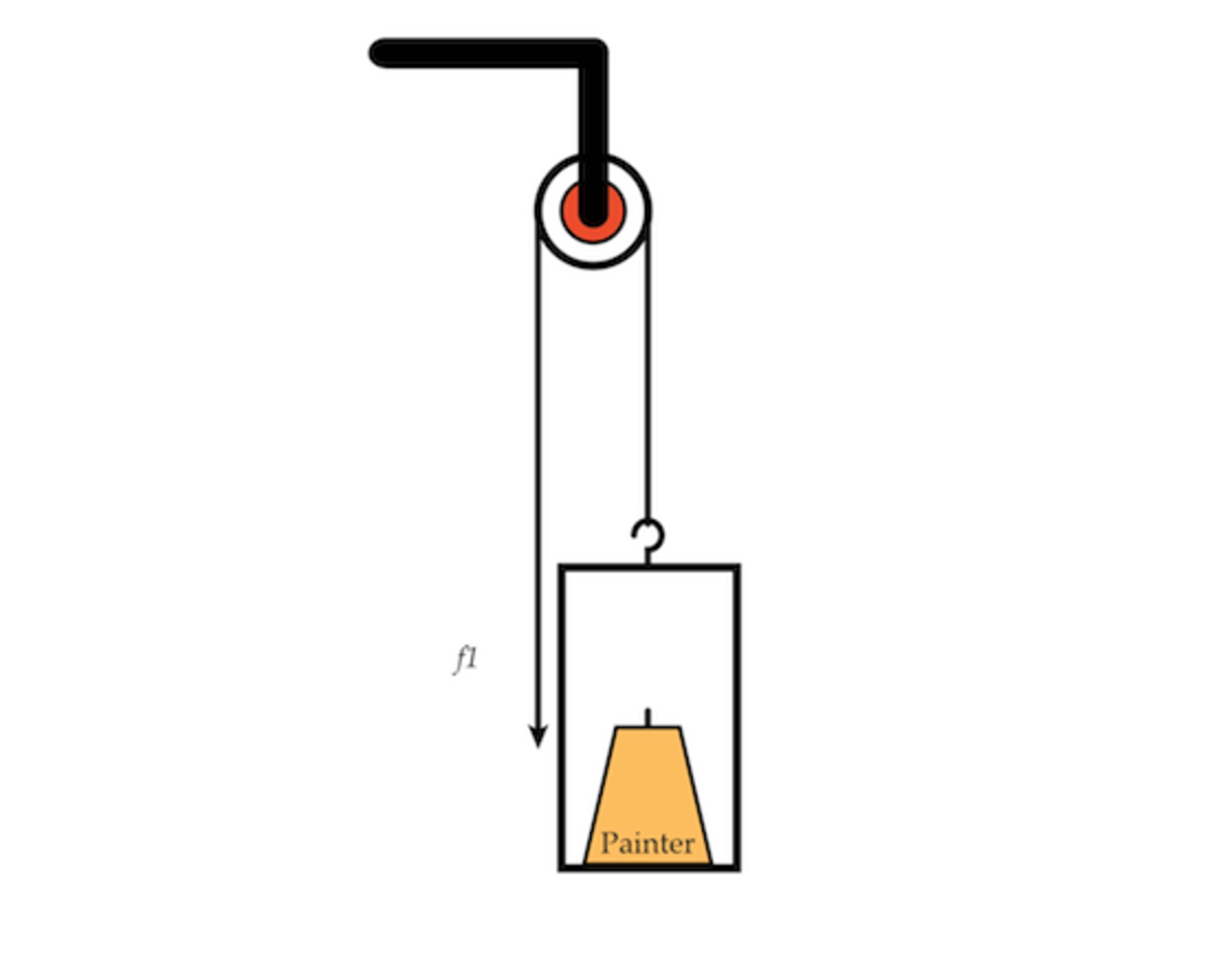
The painter's lift

If the painter pulled on a single rope, she would have to pull with the same force as the force of gravity. However, when she pulls through a pulley, the rope is connected to her at two points. Therefore, the upward force on her is actually twice the tension in the rope. So, she can pull with half as much force as if there was no pulley and still counteract gravity.

If the painter is moving upward at a constant speed, the system must be in equilibrium, and the sum of the forces must equal zero.

Considering the case with the pulley, there are two upward forces: the tension forces for the two halves of the pulley's rope. These tension forces must be the same because tension must be the same for all parts of the rope. The only downward force is the painter's weight force. The sum of these forces must equal zero.

$T+T-mg=0$

$T=\frac{mg}{2}$

Because the tension force is the force causing the painter to move, the force she exerts on the rope $F_1$ must be equal to the tension force $T$ .

$F_1=\frac{mg}{2}$

Considering the case with just one rope, there is just one upward force: the tension force, and just one downward force: the painter's weight force. Because the system is in equilibrium, the sum of these two forces is zero.

$T-mg=0$

$T=mg$

Again, because the force causing the painter to move is the force exerted on her by the rope (the tension force), $F_2=T$ .

$F_2=mg$

$\frac{F_1}{F_2}=\frac{mg/2}{mg}=\frac{1}{2}=0.5$ .

Since the mechanical advantage of a single pulley is calculated as MA = 2n, whereas n is the number of movable pulleys, the MA of the said pulley is 2. Having an MA of 2 signifies halving the effort to move the load. Therefore, the answer if 0.5 or 1/2.

First, one end of the rope is held by the painter, and the other end of the rope is held to the "lift". Assume the painter and the lift to be a single system and apply Newton's second law to the system. Note that there are 2 tensions, 2T, holding the whole system, W as the weight of the painter, and also acceleration is 0. We then have the equation below : 2T - W = 0 ( Because there is no acceleration ) T is the force of the worker exerts on the hanging rope, F1. ( T = F1 ) W is the force of the worker exerts on a single rope, F2. ( W = F2 ) Therefore, 2(F1) - (F2) = 0 (F1)/(F2) = 1/2

Since the painter is moving at a constant rate, the net acceleration is 0, which means the force exerted by the painter must exactly equal the force due to gravity. This is the same as the tension in the rope when the painter is still. Since, with a pulley, her weight is divided equally between two ropes, the tension in each is half of that of a single rope. Thus the force required for this pulley is half the force needed for a single rope.

With a single rope, the tension is equal to the painter's weight. Effectively with the rope/pulley arrangement, 2 ropes share the painter's weight. So the tension is 1/2 that of a single rope. F1 = 1/2 F2, when no acceleration is involved. (F1/F2) = 0.5.

F2 is the total force exerted by the single rope to move upward, we know that f1=the weight of the other side,so that it would keep constant, F2=F1+the weight of the other side, so F2=2F1 Thank you!

Since the rope is massless the tension in the rope is equal throughout. To move upwards using a single rope, the painter needs to pull up with a force $F_2$ equal to $F_G$ , the force of gravity on the painter. With the painter's lift, the painter pulls down on the rope with a force of magnitude $F_1$ . By Newton's 3rd law, the force the rope exerts on the painter also has magnitude $F_1$ . The other side of the rope, which is tied to the lift, also exerts a force of magnitude $F_1$ on the painter/lift. Therefore the total force on the painter/lift is $2F_1$ . This also has to be equal to $F_G$ , and so we can solve for $\frac{F_1} {F_2}=0.5$ .