The Parabolic Minimum
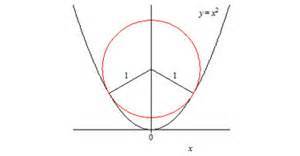
Consider the parabola obtained by rotating the curve about the axis. Consider all parabolic contains, obtained by truncating the parabola at a suitable height, which contain a unit sphere.
What is the minimum ratio of the volume of such a parabolic container, to the volume of the unit sphere?
Give your answer to 5 decimal places.
The answer is 1.89844.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let's consider P = ( t , t 2 ) , t ∈ R a generic point on the parabola. The tangent line to y = x 2 , passing through P has equation y t = m x + q , where m = d x d y = 2 x . So,
t 2 = 2 t ⋅ t + q ⟹ q = − t 2 ⟹ y t = 2 t x − t 2
Let's call y n = m ′ x + q ′ the normal line to y t . Since the two lines are prependicular, m ′ = − m 1 = − 2 t 1 . Hence,
t 2 = − 2 t 1 ⋅ t + q ′ ⟹ q ′ = t 2 + 2 1 ⟹ y n = − 2 t x + t 2 + 2 1 .
The point C we get intersecting y n and x = 0 is the center of the circle tangent to the two branches of the parabola.
⎩ ⎨ ⎧ y n = − 2 t x + t 2 + 2 1 x = 0 ⟹ C ( 0 , t 2 + 2 1 )
The radius of the circle is C P = 1
C P = ( t − 0 ) 2 + ( t 2 − ( t 2 + 2 1 ) ) = 1 ⟹ t = ± 2 3
We truncate the parabola at h = 1 + C y = 2 3 + t 2 = 4 9 . The volume of the sphere is V p = 3 4 π . The volume V p of the paraboloid generated by the rotation of the parabola around y can be easily evaluated if we consider the rotation of y = x around x .
V p = π ∫ 0 h x 2 d x = π ∫ 0 4 9 x d x = 3 2 8 1 π .
Eventually V s V p = 3 2 8 1 π ⋅ 4 π 3 = 1 . 8 9 8 4 4