The Pattern

This is a series of "Sum of Arithmetic Progression", each term listing only the final digit.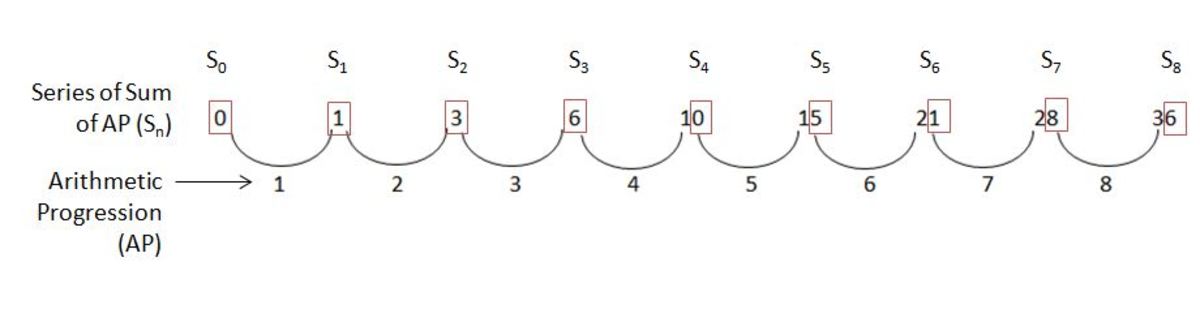

Using formula developed by mathematician: Carl Friedrich Gauss

$Sn$ = 1 + 2 + .............+ n= $\frac{n (n+1)}{2}$

For the 199th term, taking into account of 0 as the first term, n would be 198.

Applying Gauss's formula, we'd get $\frac{198 (198 + 1)}{2}$ which is 19701. Taking only the final digit, the answer is 1.

The $n$ th term is the unit digit of $\dfrac{n(n-1)}2$ ,so $\dfrac{199\times198}2=19701$ ,the answer is $1$