The pendulum
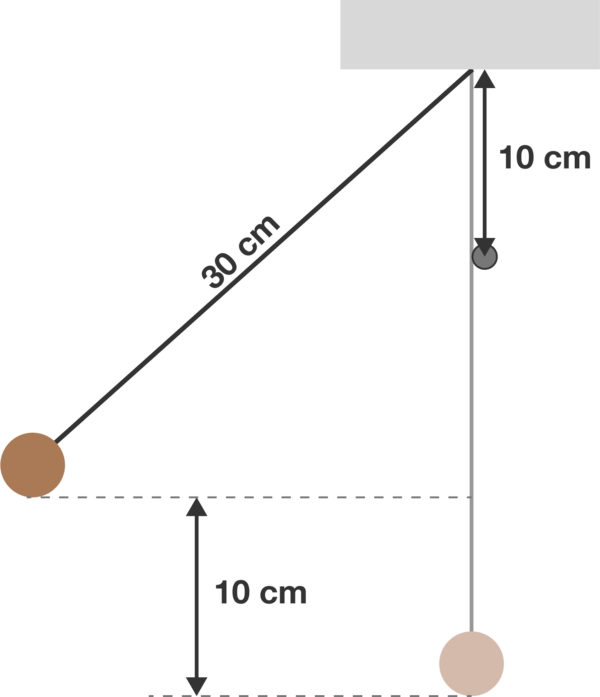
A ball hangs from a 3 0 cm string which is attached to the ceiling. A peg is nailed into the wall such that the string rests on the peg 1 0 cm down from the ceiling. Then, the ball is held up to a height of 1 0 cm from its lowest position (keeping the string taut), and then released.
Which of the following is true?
Note: Air resistance is negligible. Damping and other external forces should not be considered. Consider the ball and string to be a simple pendulum.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
but thermodynamics?
Log in to reply
You mean the second law? The question explicitly removes friction, thereby making it an idealized situation, i.e. a reversible process. For such situations the second law can be written with an equals sign. In other words, as time progresses the entropy of the system stays constant.
Only to be piky, if potential energy is the same at both points and It is a función of height this does not imply that the height is the same, to be matematicaly rigorous you must add that It is an injective function of height (since PE=mgh is clearly injective).
Am I correct in saying that you are assuming here that the string has no weight? What would happen if it did?
Log in to reply
Yes, assuming the string has no weight is the definition of a simple pendulum.
If it has weight, it's considered a "physical pendulum" instead. The "length" of the pendulum is then affected by the distribution of mass. (I'm not certain offhand what it would do to the calculations here, but when it hits the peg, you would not be including the portion above that spot in the weight for that part of the pendulum swing.)
The kinetic energy of the top part of the string is being stopped, so that could be transferred into the lower part of the system. Also looking at the lower part of the string you will see that the ball will reach its maximum height before the string. Therefore more of the potential energy will be in the ball which means the ball will be higher.
I thought energy would also be transferred to the string and the peg it is swinging off? Also, is the peg there to throw us off or is it indispensable for the solution? (serious question, apologies if what i'm saying is silly)
Log in to reply
"Damping and other external forces should not be considered"
This answer explains what the question was. I had not understood the question until I read this answer.
I'm no physicist, but doesn't this pendulum have to be in a gravitational field to move in the first place? Even if it were totally frictionless, gravity would cause each swing to be less, as it eventually would settle at the bottom. What am I missing?
Log in to reply
Gravity is necessary but it will not cause each swing to be less because gravity is a conservative force, each swing will keep all its energy (potential + kinetic). The speed gained by the pendulum during the swing is exactly enough to reach the exact same spot on the other side.
Attaching a video of Walter Levin from MIT showing this: https://youtu.be/PWNs7i4rEWA
General Comment: The question uses the word 'Ball' and the answers use the word 'Bob'.
This problem is poorly worded!
Not described well enough to understand the context. Also "bob" = "ball"
It's Bob's ball. Thankfully, he's been completely abstracted out of the diagram.
How he got into this predicament is not part of the problem, and should not be speculated about in polite (and mixed) company.
The maximum height has to be same as the initial height or else the energy of the system won't be conserved.
The initial energy of the system is K . E 1 + P . E 1 and final energy is K . E 2 + P . E 2
Where K . E and P . E are the kinetic and potential energies respectively.
For conservation of energy K . E 1 + P . E 1 = K . E 2 + P . E 2 − ( 1 )
Since it is given that the initial height of the bob is less than the peg, at its maximum height its should have zero velocity and hence K . E 2 = 0 . Also, K . E 1 = 0 since we released the bob from rest.
So equation ( 1 ) simplifies to P . E 1 = P . E 2
Since potential energy is a function of height, the final height of the bob has to be equal to the initial height.
You should add that things like air-resistance, properties of the rope, etc. should be ignored; otherwise the final height will be less than the initial height...
Log in to reply
I have done the changes. Thanks for the suggestion.
I have attempted the question before you made the changes and hence kept the wrong answer.
Energy isn't conserved in this case; Angular momentum is though. The bob should go higher. Look at the linear velocity of the bob just before and just after the the pendulum strikes the pin. call it
v
and
v
′
. Just to generalize it the pin is placed at a distance
x
below the original piviot. and apply conservation of angular momentum.
L
m
v
=
(
L
−
x
)
m
v
′
v ′ = L − x L v ...eq1.
So now the maximum potential energy at point 2 will be equivalent to the kinetic energy:
2 1 m ( v ′ ) 2 = m g h 2 , or substituting in eq1, and solving for h 2 .
h 2 = ( L − x L ) 2 2 g v 2 ...eq2.
Since L − x L > 1 , then ( L − x L ) 2 > 1 and it follows that
h 2 = ( L − x L ) 2 2 g v 2 > 2 g v 2 = h 1 for all 0 < x < L
So I think you have this wrong.
Edit: Or Angular momentum isn’t conserved and I have it wrong. Either way at this point I need some help out of the weeds on this.
Log in to reply
Angular momentum isn't conserved. You should try this yourself. Once the string hits the peg, the angular momentum increases. If the peg is low enough so the bob cannot reach it's original height, you get it to spin around the peg several times (even with air resistance). If energy wasn't conserved and the bob would go higher, you would be able to turn this entire system into an engine that gives you free energy (use a chain of the above to bring the bob to whatever height you wish, without loss of energy; then drop it down again, letting it bring up some mass; you've gotten work done without any energy cost).
Log in to reply
I think you mean the angular momentum of the bob decreases when the string hits the peg, but I see the error in my thought now. Also, they have videos of this experiment on the web. Thanks for your reply.
Frictionless pivot Agree.
While decreasing the string length will increase the maximum angular displacement of the ball, it will not change the maximum height that the ball reaches.
Bcuz when you turn the hypotenuse to 45 degrees it will be the same as the maximum height
Before releasing the ball all its energy is saved in it in form of potential energy. During the oscillation the potential energy will change as energy is transferred into kinetic energy. But we know that in all the highest points the kinetic energy has to be zero and thus, because of energy conservation, all the energy of the system has again to be in form of potential energy. As potential energy is a function of hight, the ball will exactly reach its initial hight.