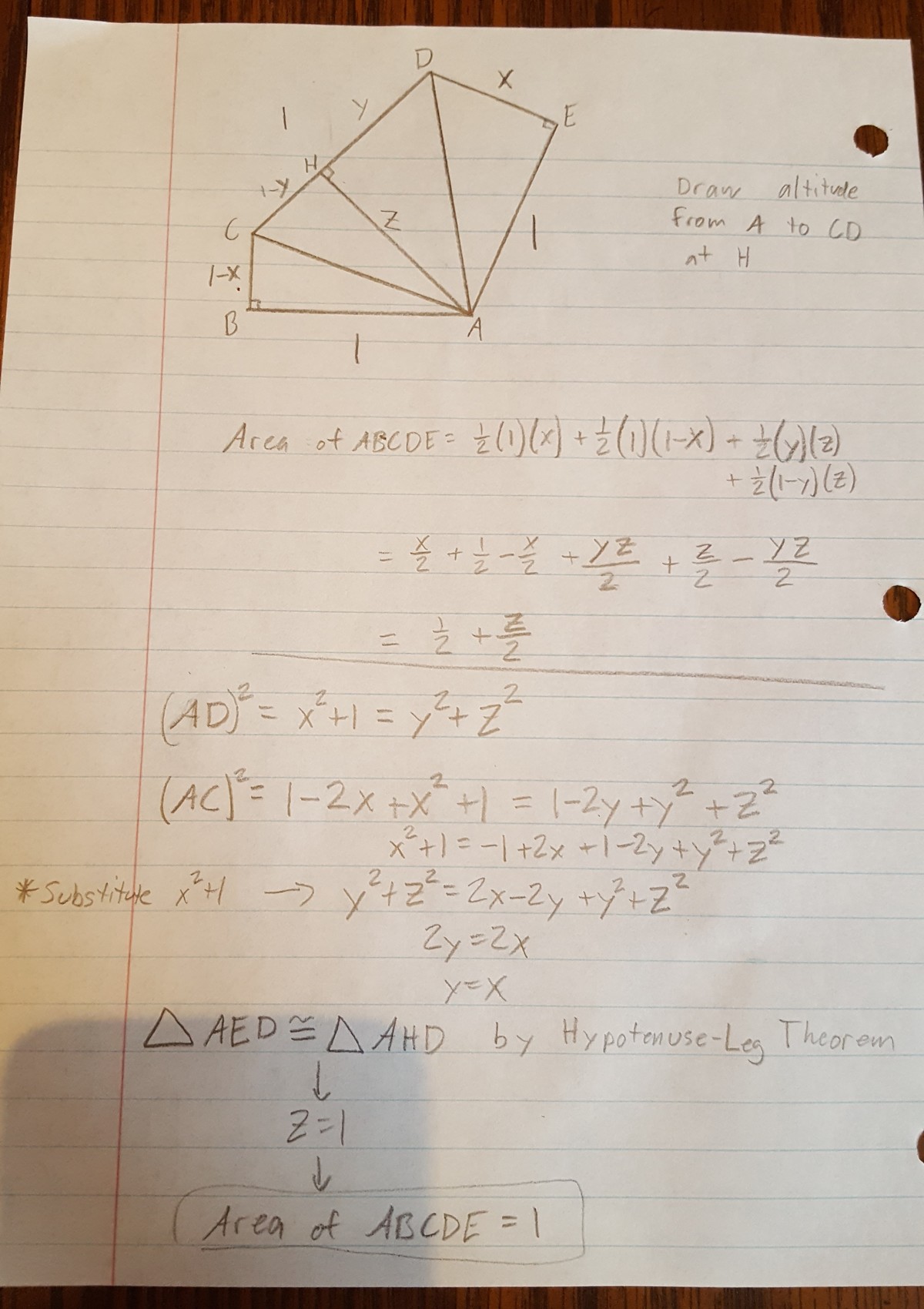The Pentagon

Geometry Level 5

In the pentagon A B C D E ABCDE , ∠ A B C = ∠ A E D = 9 0 ∘ \angle ABC=\angle AED = 90^\circ , A B = C D = A E = B C + D E = 1 AB=CD=AE=BC+DE=1 . FInd the area of A B C D E ABCDE .

Give your answer to 2 decimal places.


The answer is 1.00.

A Former Brilliant Member by A Former Brilliant Member

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

Luke Videckis
Jun 22, 2016

A different solution.

7 Helpful 0 Interesting 0 Brilliant 0 Confused

Nice one Luke. Based on your drawing, there is a pure geometric solution. We can rotate triangle ABC around A, until B coincides with E. Let's say C becomes C', then D, E, C' are collinear, and DC'=DE+EC'=DE+BC=1. Now it's easy to show that triangle ADC and ADC' are congruent by SSS, and each have area of 1/2(1)(1)=1/2, for a total area of 1.

Wei Chen - 4 years, 11 months ago

Log in to reply

Thanks for the additional insight!

Luke Videckis - 4 years, 11 months ago

Let B C = x BC=x , then D E = 1 − x DE=1-x . This means that A C = 1 + x 2 , A D = x 2 − 2 x + 2 AC=\sqrt{1+x^2},AD=\sqrt{x^2-2x+2} . The area of △ A C D \triangle ACD is given by:

S △ A C D = 1 + x 2 + 1 + x 2 − 2 x + 2 2 ⋅ − 1 + x 2 + 1 + x 2 − 2 x + 2 2 ⋅ 1 − x 2 + 1 + x 2 − 2 x + 2 2 ⋅ 1 + x 2 + 1 − x 2 − 2 x + 2 2 = 1 2 S_{\triangle ACD}=\sqrt{\frac{1+\sqrt{x^2+1}+\sqrt{x^2-2x+2}}{2}\cdot\frac{-1+\sqrt{x^2+1}+\sqrt{x^2-2x+2}}{2}\cdot\frac{1-\sqrt{x^2+1}+\sqrt{x^2-2x+2}}{2}\cdot\frac{1+\sqrt{x^2+1}-\sqrt{x^2-2x+2}}{2}}=\frac{1}{2}

At the same time,

S △ A B C + S △ A E D = x 2 + 1 − x 2 = 1 2 ∴ S A B C D E = S △ A B C + S △ A E D + S △ A C D = 1 2 + 1 2 = 1 S_{\triangle ABC}+S_{\triangle AED}=\frac{x}{2}+\frac{1-x}{2}=\frac{1}{2}\\\therefore S_{ABCDE}=S_{\triangle ABC}+S_{\triangle AED}+S_{\triangle ACD}=\frac{1}{2}+\frac{1}{2}=1

6 Helpful 0 Interesting 0 Brilliant 0 Confused
Atomsky Jahid
Jul 9, 2016

I didn't use the general case first. I imposed B C = D E = 1 2 BC=DE=\frac{1}{2} and drew a normal on CD through point A. This gave rise to 4 right triangles each having two adjacent sides [adjacent to the right angle] of length 1 and 1/2. Hence, A = 4 × ( 1 2 × 1 × 1 2 ) = 1 A=4\times(\frac{1}{2}\times1\times\frac{1}{2})=1 But, the problem stated to provide an answer having 2 decimal places. Then, I got suspicious and proved the general case. But, I'm not typing it here as other solutions depict that.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...