The Pentagon
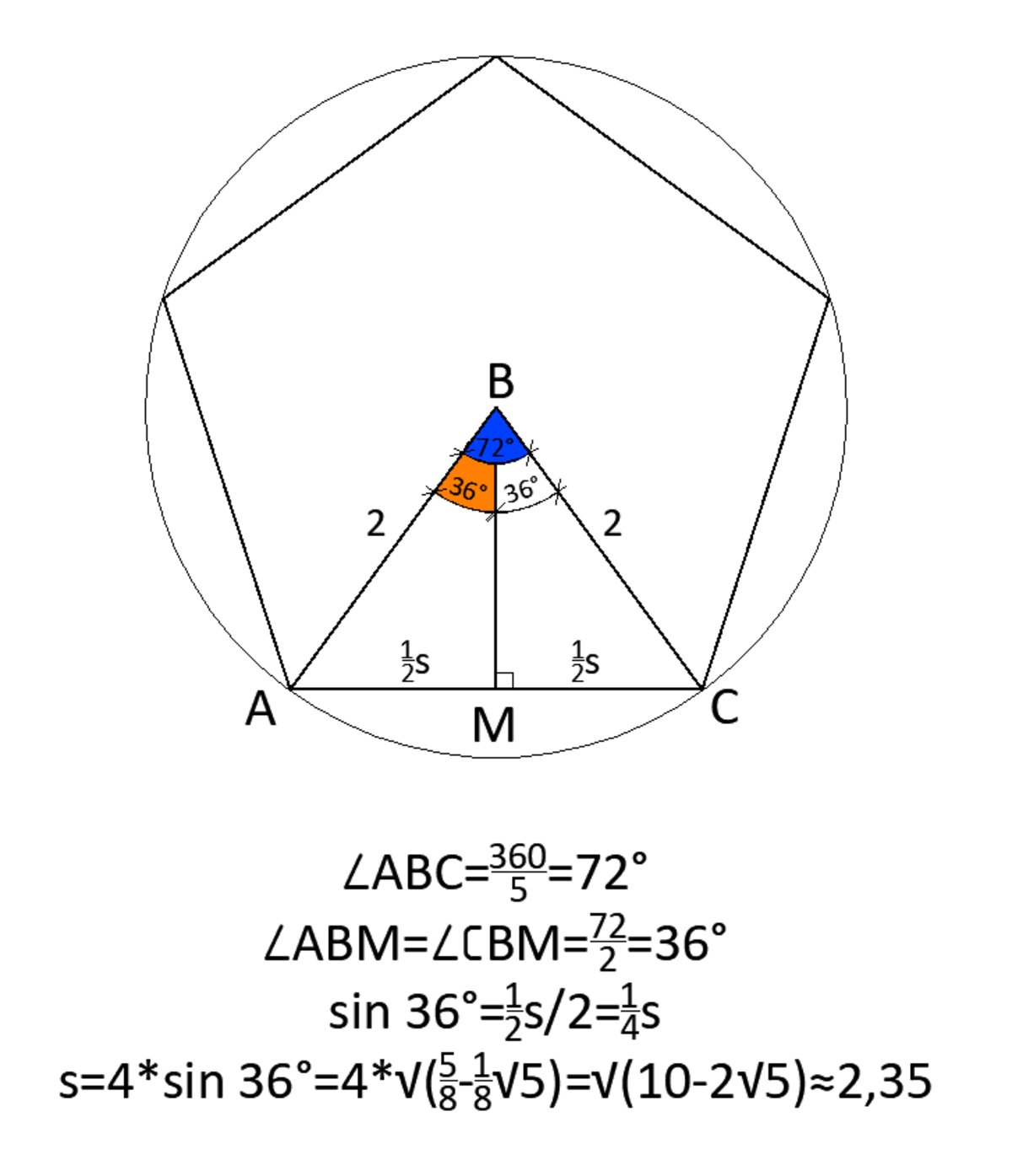
 Find the length of a side of a regular pentagon that is inscribed in a circle of radius 2.
Find the length of a side of a regular pentagon that is inscribed in a circle of radius 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
You've drawn the circle wrong, the pentagon is supposed to be inscribed in the circle. That then gives you the length of 2 for the two legs of the triangle.
Now you've got a isosceles triangle with two base angles of 54°, a top angle of 72° and a height of 2. That would give you 1/2x=2/tan 54° so x=4/tan 54°=2,9.
Draw two radii passing through two consecutive vertices of the regular polygon. Now the angle between them is 360/5=72°… making a room for cosine formula, which would result in easy solution.
Not a four level problem!!
Well, that's an easier solution. :D
That will show that sin 3 6 ∘ = 8 5 − 5 and cos 3 6 ∘ = 4 1 + 5 . Can you prove that? :)
x 2 = 2 2 + 2 2 − 2 ( 2 ) ( 2 ) cos 7 2
x 2 = 8 − 8 ( 4 5 − 1 )
x 2 = 8 − 2 ( 5 − 1 )
x 2 = 8 − 2 5 + 2
x 2 = 1 0 − 2 5
x = 1 0 − 2 5