The Perfect Straw

Geometry Level 2

Peter is a manufacturer for a dining franchise. He is trying to design a cup and straw that will fit perfectly, and his boss gave him some requirements:

  • The cup must hold exactly 45 cubic inches of water when full.
  • The cup must be perfectly cylindrical.
  • The cup must be 7 inches tall.
  • When the straw is packed as tightly as possible, 1.5 inches of it must be sticking out of the cup.

How long must the straw be, to the nearest hundredth of an inch?

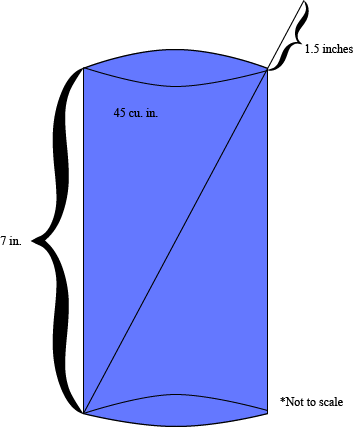Image for reference Image for reference


The answer is 9.06.

Blan Morrison by Blan Morrison , 18, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Steven Chase
May 9, 2018

Radius calculation based on height and volume:

V = π r 2 h 45 = π r 2 ( 7 ) r = 45 7 π V = \pi r^2 h \\ 45 = \pi r^2 (7) \\ r = \sqrt{\frac{45}{7 \pi}}

Diagonal length:

L 2 = ( 2 r ) 2 + h 2 L = 4 r 2 + h 2 = 180 7 π + 49 L^2 = (2r)^2 + h^2 \\ L =\sqrt{4 r^2 + h^2 } = \sqrt{\frac{180}{7 \pi} + 49 }

Straw length:

L s = L + 1.5 = 180 7 π + 49 + 1.5 ≈ 9.06 L_s = L + 1.5 = \sqrt{\frac{180}{7 \pi} + 49 } + 1.5 \approx 9.06

3 Helpful 0 Interesting 0 Brilliant 0 Confused

@Steven Chase , we really liked your comment, and have converted it into a solution. If you subscribe to this solution, you will receive notifications about future comments.

Brilliant Mathematics Staff - 3 years, 1 month ago

Log in to reply

Sounds good, thanks

Steven Chase - 3 years, 1 month ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...