The Perfect Tangential Match
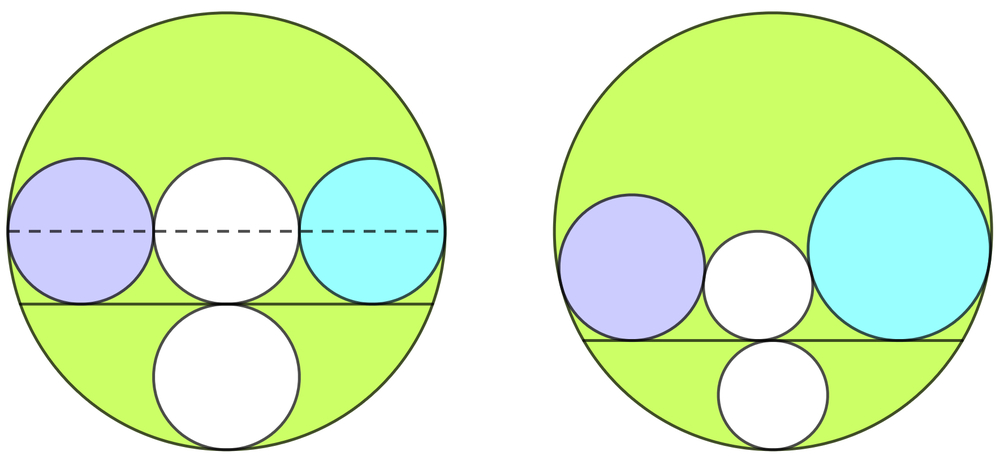
In the green circle, the white circle is drawn tangent to the chord and the arc, and also centrally positioned on the chord. Another white circle is drawn inside, and also tangent to the chord and purple and blue circles, each also tangent to both the arc and the chord.
As shown on the left, the diameter sum of one white, one blue and one purple circles, all having congruent radii, is the diameter of the green circle. Does that hold for any other circle and chord arrangement?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Nicely written generalization to the given problem. What is geometric about this problem is that the circle arrangement resembles a quadrilateral of two pairs of opposite parallel sides (involving the radius of the green circle bisecting the purple and the blue circles).
Label the diagram as follows, where G is the center of the green circle, P is the center of the purple circle, W is the center of the white circle, and B is the center of the blue circle:

Let g be the radius of the green circle, p be the radius of the purple circle, w be the radius of the white circle, and b be the radius of the blue circle.
Then P W = p + w , P K = P N − K N = P N − W O = p − w , and by the Pythagorean Theorem on △ P K W , K W = P W 2 − P K 2 = ( p + w ) 2 − ( p − w ) 2 = 2 p w .
Also, B W = b + w , B M = B R − M R = B R − W O = b − w , and by the Pythagorean Theorem on △ B M W , W M = B W 2 − B M 2 = ( b + w ) 2 − ( b − w ) 2 = 2 b w .
In addition, P G = D G − P D = g − p , A P = A N − P N = G Q − P N = G S − Q S − P N = g − 2 w − p , and by the Pythagorean Theorem on △ P A G , A G = P G 2 − A P 2 = ( g − p ) 2 − ( g − 2 w − p ) 2 = 2 w ( g − p − w ) .
Also, G B = G H − B H = g − b , C B = C R − B R = G Q − B R = G S − Q S − B R = g − 2 w − b , and by the Pythagorean Theorem on △ B C G , G C = G B 2 − C B 2 = ( g − b ) 2 − ( g − 2 w − b ) 2 = 2 w ( g − b − w ) .
Since A C = K M , A G + G C = K W + W M , or 2 w ( g − p − w ) + 2 w ( g − p − b ) = 2 p w + 2 b w , which simplifies to g = b + p + w or 2 g = 2 b + 2 p + 2 w .
Therefore, the diameter of the green circle is always the sum of the diameters of the blue, purple, and white circles.
I'm sure there's a beautiful geometric proof for this, but meanwhile here's a clunky coordinate geometry one:
Say the green circle has unit radius and is centred at ( 0 , 0 ) . Let the white circles' radii be w . We'll use w and p (the x -coordinate of the upper white circle's centre) as parameters.
The equation of the chord is y = 2 w − 1 .
Since the upper white circle is tangent to the chord, its centre is ( p , 3 w − 1 ) .
The trick here is to note that, algebraically, there's no real difference between the blue and purple circles. Both have to
The fact that one is to the left and one to the right is just labelling. The idea is to exploit this symmetry; these conditions should lead to two possible solutions, one for each circle.
Say a circle satisfying the above conditions has radius R and its centre has x -coordinate q . The conditions above become (respectively):
From the second condition, q = p ± 2 R w
Substituting into the third, ( p ± 2 R w ) 2 = 4 w − 4 w 2 − 4 R w
Clearing the square root leads to 6 4 R 2 w 2 + 6 4 R w 3 − 6 4 R w 2 + ( p 2 − 4 w + 4 w 2 ) 2 = 0
which looks horrible, but is in fact just a quadratic in R (with two solutions, as expected). By Vieta, the sum of the roots is 6 4 w 2 6 4 w 2 − 6 4 w 3 = 1 − w
But the sum of the roots is just the sum of the two radii; ie the radii of the blue and purple circles in the diagram. Hence the sum of the radii of the blue, purple and white circles is just 1 , the radius of the green circle, so the statement is always true .