The Perimeter Is A Useful Information?
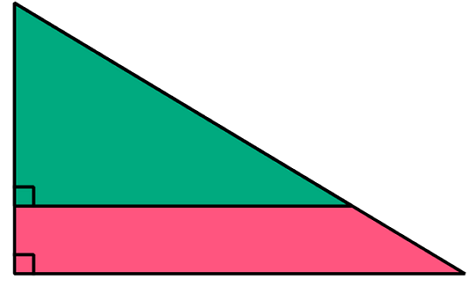
The above shows two similar right triangles. The side lengths of the green right triangles are 9, 12 and 15.
Given that both the perimeter of the green region and the pink region are equal, find the area of the entire figure (green and pink regions).
The answer is 96.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Perimeter of the big triangle (made out of the green and pink sectors)= 2×36 - 2 × 12 = 48
How do you know this is true?
Log in to reply
The perimeter of the big triangle is the sum of the perimeters of the pink and the green sectors (36×2) - the length of the line forming the border between these sectors (12, twice as we counted it in both the perimeters of the green and the pink sectors, but now it is inside the big triangle, therefore it is not part of its perimeter.)
Is it just me or anyone else get 2 solutions for this question? Because it did not specify which side that was shared between those shapes. I'm getting 96 and 121.5.
Relevant wiki: Similar Triangles Problem Solving - Basic
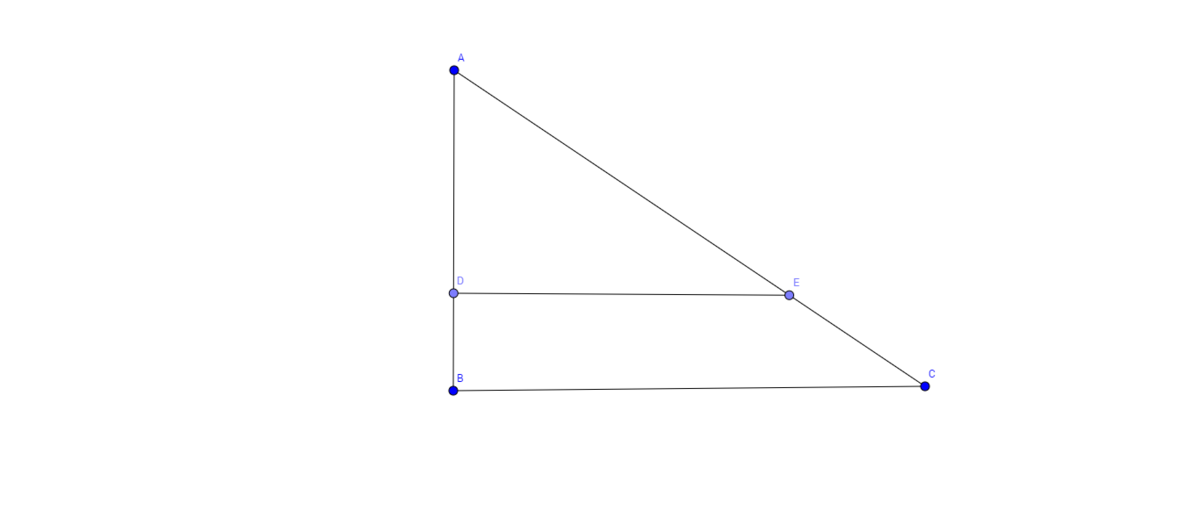
Let
D
B
=
x
,
B
C
=
y
and
C
E
=
z
.
According to the question,
x
+
y
+
z
+
1
2
=
9
+
1
2
+
1
5
⇒
x
+
y
+
z
=
2
4
⇒
z
=
2
4
−
x
−
y
−
−
−
−
−
1
Due the similarity in
△
A
D
E
and
△
A
B
C
,
9
9
+
x
=
1
2
y
⇒
3
y
−
4
x
=
3
6
−
−
−
−
−
2
1
5
+
z
1
5
=
y
1
2
⇒
5
y
−
4
z
=
6
0
−
−
−
−
−
3
9
+
x
9
=
1
5
+
z
1
5
⇒
z
=
3
5
x
−
−
−
−
−
4
Substituting equation
(
1
)
in
(
4
)
,
we get
3
5
x
=
2
4
−
x
−
y
⇒
8
x
+
3
y
=
7
2
−
−
−
−
−
5
Now equation
(
2
)
and
(
5
)
are simultaneous equations.By solving it,we get
x
=
3
and
y
=
1
6
.
z
=
2
4
−
x
−
y
=
2
4
−
3
−
1
6
=
5
.
Therefore the area of the whole figure
=
2
1
×
(
9
+
x
)
×
y
=
2
1
×
1
2
×
1
6
=
9
6
.
If scale factor from small triangle to large is k then sides of quadrilateral clockwise are 12 , 15k-15, 12k and 9k-9. Perimeter of small triangle is 9+12+15=36. Perimeter of quadrilateral is 36k-12. 36k-12=36 so k=4/3. Area scale factor is (4/3)^2 = 16/9. Small triangle area is 54 so full area is 54×16/9. Full area = 96.
use trigonometry:
1) take bottom right angle as theta.
2) find sin theta and cos theta
3) you will get ratio of sides in the form of one of the sides after solving
4) get area of the whole triangle when you get all the values of sides from step 3
by Pythagorean triples and ratio: this is 3:4:5 where the fractional value is 3 for 9,12 and 15. By logic, the next possible value for fractional value is 4 which makes the sides 12,16 and 20. thus the area = 0.50(12)(160) = 96
Perimeter of the green triangle = 9 + 12 + 15 = 36
Perimeter of the big triangle (made out of the green and pink sectors)= 2×36 - 2 × 12 = 48
Scale factor = 48/36 = 4/3
Side lengths of the big triangle: 12, 16, 20
Area of the big triangle = 12 × 16 / 2 = 96