The perimeter is

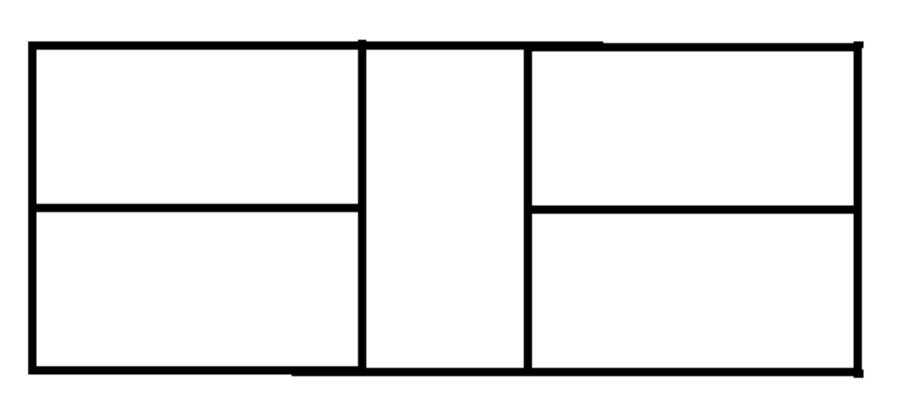
Let $a$ and $b$ be the lengths of the short side and long side of the small rectangle respectively. Then $ab=8$ . Since the large rectangle has five small rectangle its area is $40$ and we have:

$\begin{aligned} 2a(2b+a) & = 40 \\ a(2b+a) & = 20 \\ 2ab + a^2 & = 20 \\ 16 + a^2 & = 20 \\ a^2 & = 4 \\ \implies a & = 2 & \implies b = \frac 8a = 4 \end{aligned}$

Since the perimeter of the large rectangle is $2(2a+2b+a) = 2(4+8+2) = \boxed{28}$ .

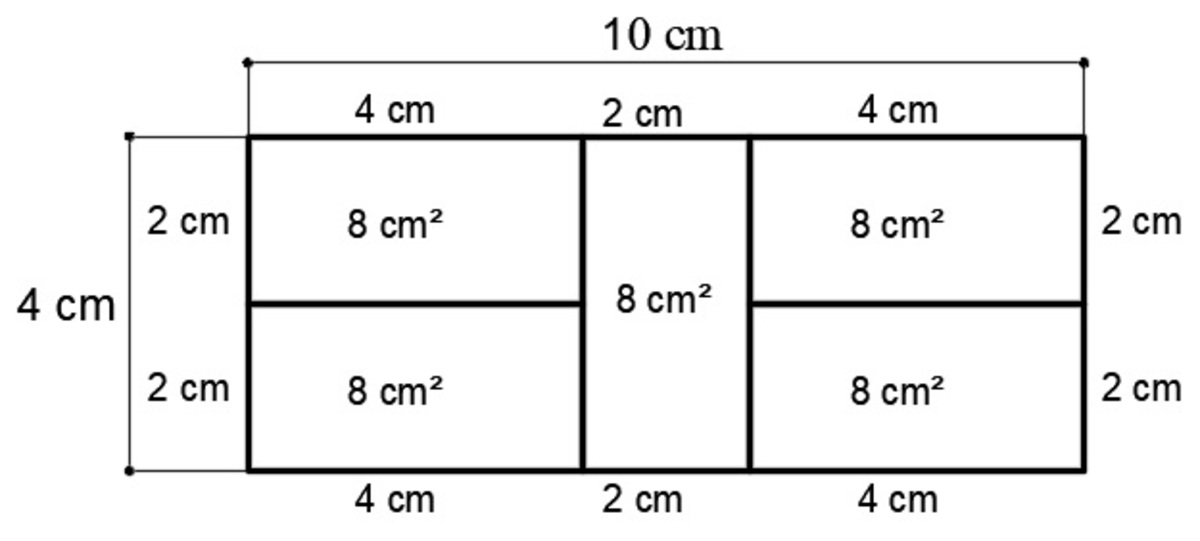
Let the shorter side of one small rectangle be $\text{2 cm}$ and the longer side be $\text{4 cm}$ . So the perimeter of the big rectangle is

$P=2(4) + 2(10)=\boxed{28}$

It is not given that all the 5 rectangles are congruent. Let us suppose corner rectangles of dimensions 1 by 8 and middle rectangle of dimension 2 by 4. Then perimeter of big rectangle is coming to be 44. It should be mentioned that rectangles are congruent.

• Height of the vertical rectangle = Twice of Width of horizontal rectangle $\implies$ dimensions are $x, 2x$
• $x \times 2x = 8 \implies x = 2$
• Perimeter is $(x + 2x)\times 4 + 2x = \boxed{28}$