The physics of rah-rah
Cheerleaders at sporting events will often use a bullhorn to make themselves louder. A bullhorn is simply a hollowed out cone - you speak into the narrow end and your voice comes out the wide end, channeled by the cone so it is louder than it would be otherwise. At a sporting event, a cheerleader holds a bullhorn up to their mouth as in the figure below. The very tip of the bullhorn rests on their mouth and they use their hand on the other end to hold the bullhorn horizontal and still. We model the bullhorn as the rigid 2-d hollow cone of horizontal length 0 . 7 5 m , opening angle 3 0 ∘ , and (surface) mass density of 0 . 4 kg/m 2 (see figure). How much force in Newtons does the cheerleader exert at point A?
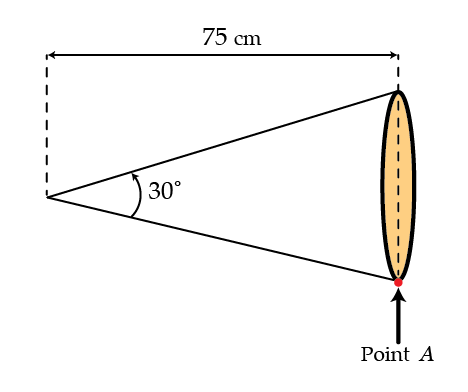
Details and assumptions
- You may take g to be 9 . 8 m/s 2 .
- Assume the force at point A is directed straight up.
The answer is 1.28.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Consider the tip of the bullhorn. The net torque acting around this point is τ g + τ c , where τ g is the torque due to gravity and τ c is the torque exerted by the cheerleader. Note that τ g = − m g C , where m is the mass of the bullhorn, g is the acceleration due to gravity, and C is the distance of the center of mass to the tip of the bullhorn. It is known that for a cone with length l , the distance from its center of mass to the tip is 3 2 l . Also note that the net torque acting on the tip is 0 , as it is in rotational equilibrium. Hence, τ c = 3 2 m g l . Let θ be the angle between the edges of the cone. Choose the origin as the tip of the horn and let the x axis be the axis of the bullhorn. Let σ be the density of the bullhorn. Then, note that the mass of the bullhorn will be σ 0 ∫ l sin 2 θ 2 π x = σ sin 2 θ π l 2 . Plugging this value in our first equation, we obtain τ c = σ 3 2 l sin 2 θ π l 2 g . However, note that the torque exerted by the cheerleader is also equal to F A l . Equating these, we obtain: F A l = σ 3 2 l sin 2 θ π l 2 g ⟹ F A = σ 3 2 sin 2 θ π l 2 g Plugging the values, we find out that F A = 1 . 2 8 N .
Oops, forgot to put the integration variable within the integral. It should have been:
m = σ 0 ∫ l sin 2 θ 2 π x d x
Very sorry for the mistake.
Solution 1 Taking the pivot point of the bullhorn at the mouth, the problem is asking to find a torque produced at Point A such that it equals the torque produced my the mass of the bullhorn. Using simple trig, we can deduce that the radius of the base is r = . 2 0 0 9 6 m e t e r s .
To calculate the first moment set up its surface integral Surface ∮ ∮ z J σ d A , where J is the Jacobian from the parametrization of the cone. In general, a description of a cone is z 2 = C ( x 2 + y 2 ) . To find the value of C, use the similar triangle and the relation t a n ( θ ) = z x , where θ = 1 5 . Using the formula for the Jacobian for , we get roughly 3 . 8 6 3 7 . Call this constant D . Now, substitute the value of the Jacobian into the surface integral and set up the integral with limits in polar coordinates.
∫ 0 2 π ∫ 0 r D C σ r 2 d r d θ = 3 σ C D r 3 2 π = M z .
Using the relation M z × g = R × F with R = . 7 5 m e t e r s , we get F = 1 . 2 8 N
(Note: we are balancing the torque using the center of mass as the moment arm of the weight. But, because the mass cancels out in the equation, we only need to calculate the integral, also called the first moment.)
1) Force is applied at point A to prevent the
Torque
produced by the gravity at the cone's
center of mass (which is at a distance of
3
2
h
from the vertex).
2) Balance the torque of both the forces (i.e, Mg and F) taking the vertex as axis of rotation.
3) The torque-balance equation is as follows:
M g × 3 2 h = F × h
4) Solving the equation, we get
* F= 3 2 M g *
5) M = S u r f a c e M a s s d e n s i t y × S u r f a c e A r e a
6) Surface Area = 3 . 1 4 × R a d i u s × h 2 + r 2
[where radius = h tan θ (theta=15 degrees)]
Simplifying and multiplying the surface area with Mass density, we get the value of 'M'.
6) Plug in the values of M and g in the equation * F= 3 2 M g * and get the value of F .
Ans: 1.28
P.S- Sorry, for I haven't provided the simplifications at each and every step as the motive of my solution is to make you understand the concept. (Believe me, this problem needs a calculator and plug in the values only after you reach the last step; otherwise you are gonna have a hell of a tough time simplifying at each step.);
To find the position of the center of mass of the hollow cone, we let treat the cone as many infinitesimally thin rings. Suppose each ring has a mass (\dm) , then by similarity,
d m = p 2 π h R z d z
Whereby p is the mass density, R is the radius of the cone, H is the height of the cone, all of which are just constants which are easily determined using simple geometry.
Now we integrate z with respect to dm, so we get
∫ 0 h z d m = p 2 π h R ∫ 0 h z 2 d z = p 3 2 π R h 2
Then, to get the center of mass we divide the result of the integration by M = p π R h . SO we get x c o m = 3 2
Next, equate the moments of the weight and the force exerted by the cheerleader (F) about the mouth. So immediately solve for F,
( p π R h ) ( g ) ( 3 2 h ) = F h , F = 1 . 2 6 N
Very close to the answer given (LOL?) but never mind I hope this works :)
The formula for mass is 2 σ s l , where s is the length of the arc in radians and l is the slant height. This is based off the geometric definition of a cone, which is a sector of a circle. Your formula seems more like the lateral surface area of a cylinder.
correction, 2 / 3 h !
First we need to find the centre of mass of the hollow cone, let the angle between the lateral height l and height h be θ and the mass density be σ
Consider an ring of mass d m of the cone with infinitesimal horizontal length d x , the infinitesimal segment on the lateral height is thus c o s θ d x
d m = σ d A = σ ( 2 π c o s θ t a n θ ) x d x ,
Formula for centre of mass is given by x c m = M ∫ 0 M x d m
Substitute d m with d x
x c m = σ π r l ∫ 0 h ( 2 π σ c o s θ t a n θ ) x 2 d x = h 2 2 ∫ 0 h x 2 d x = 3 2 h
By symmetry, the centre of mass should lie on the height of the cone, 3 1 h from the base
Balancing the torque,
F required equals h M g ∗ 3 2 h = 3 2 ( σ π c o s θ t a n θ h 2 ∗ g )
Plugging in the values with θ = 1 5 ∘ , h = 0 . 7 5 , σ = 0 . 4 , g = 9 . 8 ,
We obtain the final answer F = 1 . 2 8 N