The physics of toilet paper
A toilet paper roll of mass m = 1 5 0 g with inner radius r = 1 . 5 cm and outer radius R = 5 cm is put on a small cylindrical bar with coefficient of friction k = 2 . If we pull the paper straight down very slowly and increase the force very gradually, the inner part of the roll will first move without slipping on the bar. Then at some critical force F c , it will start to slip. Assume that the pulled out piece of paper is always vertical. Find F c in Newtons .
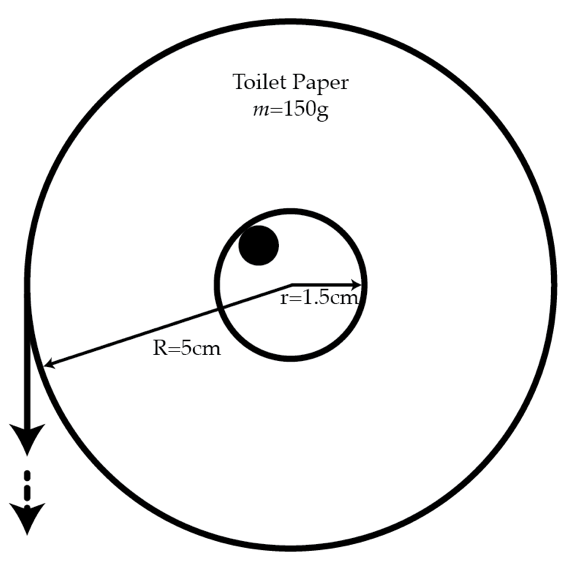
Details and assumptions
- The gravitational acceleration is g = − 9 . 8 m/s 2
The answer is 0.539.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Since the paper is pulled down very slowly and the force starts increasing gradually(slowly also); there is a static friction force developed in the small support(cylindrical bar). In the limiting case of static friction, we know that f (i.e the friction force) = kN (here N is normal contact force & k is given friction coefficient).
f = kN ...(i)
We know that normal force acts perpendicular to surface of contact. Therefore N acts perpendicular to cylindrical bar. Let N make an angle 'p' with vertical. We know f acts along the surface of contact. Mg will act downwards. And its given that F acts downward too. Resolving f and N along horizontal and vertical we write the translational and rotational equilibrium equations.
Writing the equilibrium equation in the vertical, we get
Mg = Ncos(p) + fsin(p) - F ........ (ii)
Writing along horizontal, we get
fcos(p) = Nsin(p) ............(iii)
Balancing torques; we get rotational equilibrium eq.
FR=fr ........(iv)
Solving above four equations and substituting M = 150gms , r = 1.5cm , R = 5cm , k = 2 , and g= 9.8m/s^2 We get the value of F as 0.539N.
since the motion is very slow we may assume that the paper roll is always in equilibrium. From the balance of torque: F(R-r\sin\alpha) = mgr\sin\alpha (\alpha is the angle between line passing from cetre of paper roll to the bar and vertical axis) From the balance of force, the force the bar exerts on paper roll must be vertical, i.e it forms with the normal at contact point an angle \alpha. Since the coefficient of friction is k=2, the critical value of \alpha is \arctan{2} (friction/normal force=k) Thus critical value of F is F=mg\frac{r\sin\alpha}{R-r\sin\alpha}=0.539
The physics of toilet paper
We choose a Cartesian reference frame with the origin in the contact point between the internal cylinder and the small bar (black circle). Let θ be the angle between the vertical y axis and the line connecting the bar with the center of mass of the toilet paper roll. The forces acting on the roll are: Mg (weight) F (force exerted pulling the paper) N (normal reaction produced by the rod) T (tangential force caused by friction)
The equations of motion for the center of mass are:
mx ̈=Tcosθ-Nsinθ
my ̈=Tsinθ+Ncosθ-F-mg
and the equation of the angular momentum, calculated at the contact point between the roll and the bar, is:
Iθ ̈=F(R-r senθ)-mgr sinθ
where I is the moment of inertia of the roll around the bar.
We know that the tangential friction force T must be related to the normal force N by the following relation:
T≤kN
When the roll starts to slip the angle θ and the x and y coordinates of the center of mass remain constant, so that:
x ̈=y ̈= θ ̈=0
and the tangential friction force reaches the limit value T = kN . With these assumptions, and indicating with θc the constant critical angle, the first and the third equations become respectively:
kNcosθc-Nsinθc=0
Fc(R-r senθc )-mgr sinθc=0
From the first one we find:
tanθc=k
and from the second one:
Fc=(mgr sinθc)/(R-r senθc )
Substituting the numerical values, we have:
θc = arctan (2) = 63.435°
and finally:
Fc = (0.15×9.8×0.015×sin(63.435°))/(0.05-0.015 sen(63.435°)) = 0.539 Newtons
The are 3 forces acts on the toilet paper roll: the gravity force P = m g , the pulling force F c and the force at the contact point between the roll and the bar F . Since the first 2 forces are vertical, the 3rd one must also be vertical. Since the friction coefficient is k , the angle c must satisfy tan c = k or sin c = 1 + k 2 k ) when the roll starts to slip.
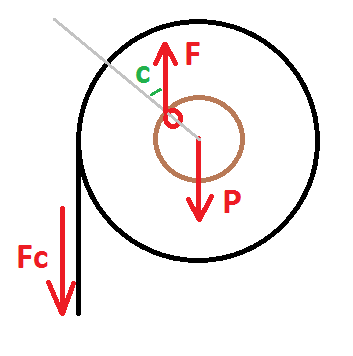
In the horizontal direction, the distance between the contact point to the P -vector is r sin c = 1 + k 2 k r while the distance between the contact point to the F c vector is R − r sin c = R − 1 + k 2 k r , so for the torque condition to be 0 for slow motion, one needs:
F c = R − r sin c r sin c P = R − 1 + k 2 k r 1 + k 2 k r m g = 0 . 5 3 9 N
Assume that the roll has reached the angle at which the pulling force balances the gravitational tug on the roll. This static roll sees no net force or torque. We therefore have three balancing conditions: the vertical forces, the torques about the pivot, and the forces along the plane of contact between the roll and the bar.
Draw a line from the center of mass of the roll (the center of the inner circle) to the point of contact with the bar and call the angle that this line makes with the horizontal γ .
Torque
The force of pulling F c and the gravitational torque m g balance each other about the pivot at the bar. The moment arm for the pulling force is given by the horizontal distance from the center of mass of the roll to the pivot which is given by r i n n e r cos γ . The moment arm for the pulling force equals the horizontal distance between the edge of the roll to the pivot which is given by r o u t e r − r i n n e r cos γ . Therefore, the balance of torque about the pivot is given by:
m g r i n n e r cos γ = F_c r o u t e r − r i n n e r cos γ ).
Vertical forces
Call the normal force from the roll to the pivot N which is directed perpendicularly from the roll to the bar at the angle g a m m a with respect to the horizontal. This also creates a force of friction k N which points along the plane of contact between the roll and bar. The normal force contributes the vertical component N cos γ and the force of friction contributes a vertical component k N sin γ , both pointing upward. The pulling force and the gravitational pull each point in the vertical direction downward. The balance of vertical forces is therefore given by:
F c + m g = N cos γ + k N sin γ
Force along the plane of contact
Along the plane, the force of friction exerts a force k N to the right while the pulling force and gravitational pull contribute a force ( m g + F c ) cos γ to the left. To maintain the no-slip condition, the frictional force must exceed the force of the pull and gravity. This condition is given by:
k N ≥ ( m g + F c ) cos γ .
The first two of these relations provide us with a way to solve for γ and N in terms of F c and the last tells us when the friction is overcome by the force of pulling.
From the torque condition, it is easy to find c o s γ in terms of F c : cos γ = r i n n e r r o u t e r 1 + m g / F c 1 .
From the balance of vertical forces, we find that the normal force is given by:
N = k cos γ + sin γ F c + m g .
In the following calculation, we let cos γ = x and sin γ = 1 − x 2 .
At the point where the force of friction is overcome by the pulling force, F c , the inequality becomes an equality, i.e.
k N = ( m g + F c ) cos γ
Substituting for N and cos γ we have:
k k x + 1 − x 2 F c + m g = ( F c + m g ) x
Dividing through by F c + m g , multiplying through by k x + 1 − x 2 and isolating the root term on its own side of the equation, we find:
k − k x 2 = x 1 − x 2 .
This results in the quartic polynomial equation
x 4 − k 2 + 1 2 k 2 + 1 x 2 + k 2 + 1 k 2 = 0 .
This relation is just a quadratic in x 2 .
The roots of the quadratic must add to k 2 + 1 k 2 and sum to k 2 + 1 2 k 2 + 1 . This suggests two roots at x 2 = 1 and at x 2 = k 2 + 1 k 2 .
The root at 1 suggests x = x 2 = 1 → cos x = 1 which implies that γ = π / 2 . This solution corresponds to the state where there is no pulling force, i.e. F c = 0 where the roll hangs straight up and down.
We therefore take the second solution x = k 2 + 1 k to correspond to the pulled state which implies γ = arccos k 2 + 1 k = arccos 5 2 . This is the angle that the center of mass of the roll makes with the bar when the critical force F c is applied.
With this solution in hand, we can use the torque equation one more time to calculate the value of F c , the critical pulling force.
F c = r o u t e r − r i n n e r cos γ m g r i n n e r cos γ = r o u t e r − r i n n e r 5 2 m g r i n n e r 5 2 ≈ 0 . 5 3 9 Newtons .