The Prime Life of Hexagon Flowers

Let the number of hexagons in a $n$ -row flower be $a_n$ and $a_1=1$ . Then we note that:

$\begin{aligned} a_{n+1} & = a_n + 6n \\ a_{n+1}-a_n & = 6n \\ \sum_{k=1}^n \left(a_{k+1}-a_k\right) & = \sum_{k=1}^n 6k \\ a_{n+1} - a_1 & = 3n(n+1) \\ a_{n+1} & = 3n(n+1) + a_1 \\ & = 3n(n+1) + 1 & \small \color{#3D99F6} \text{Replace }n \text{ with }n-1 \\ \implies a_n & = 3n^2 - 3n + 1 & \small \color{#3D99F6} \text{for }n \in \mathbb N \end{aligned}$

And $a_6 = 91 = 7 \times 13$ is a composite or non-prime .

The number of hexagons with $n$ rows can be expressed as $2(\frac { 2n(2n-1) }{ 2 } -\frac { n(n-1) }{ 2 } )-(2n-1)$ .

Simplifying gives $4{ n }^{ 2 }-2n-{ n }^{ 2 }+n-2n+1$ , and then finally $3{ n }^{ 2 }-3n+1$ .

For values of $n$ from 2 to 5, this gives a prime number, however with $n=6$ it gives 91, which is divisible by 13 and 7.

Long explanation can be found here: The Prime Life of Hexagons

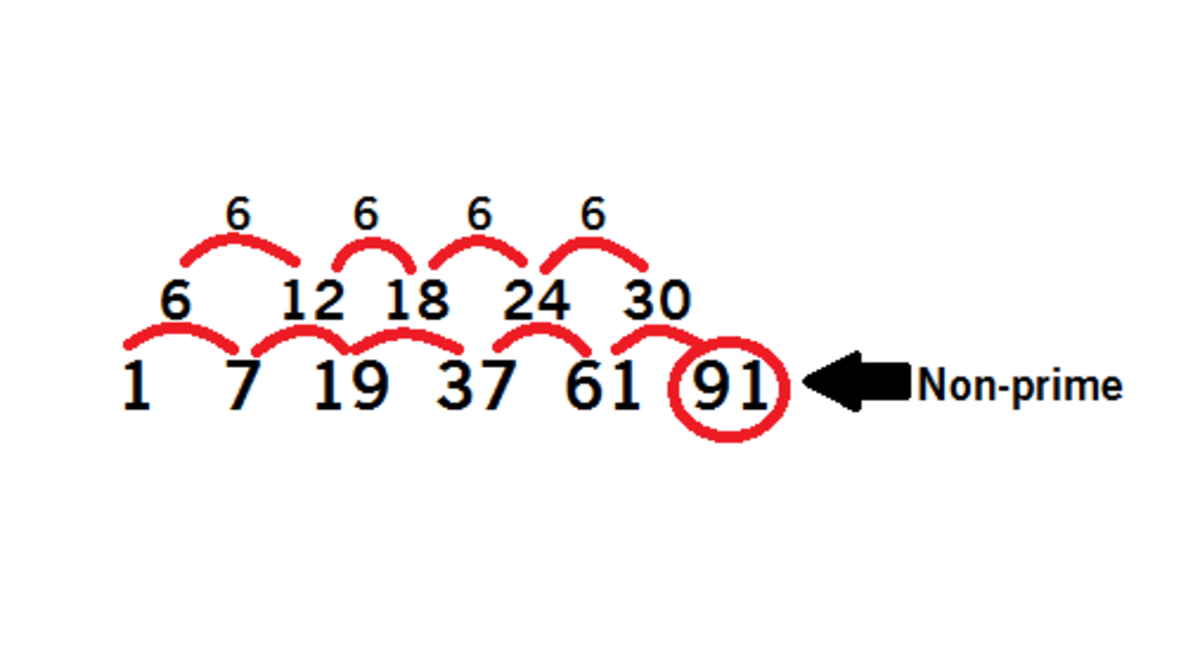
In a nutshell: We can see that the total amount of hexagons needed is always one more than a multiple of six:

• 2 rows: $7 = 6\times 1 + 1$

• 3 rows: $19 = 6\times 3 + 1$

• 4 rows: $37 = 6\times 6 + 1$

• 5 rows: $61 = 6 \times 10 + 1$

So all of these are prime, because for a number one bigger than a multiple of 6 (which is therefore divisible by two, three and other 2-/3-multiples), finding divisors is much harder, as 2, 3, 6 and so on will not work. And no divisors but one and the number itself are the definition of primes.

However if we go on and make our hexagon bigger, we get 91 hexagons. And 91 is divisible by 1, 7, 13 and itself.

6 rows: $91 = 6\times 15 + 1$

So yes, it is possible, although primes occur frequently in this series. :)

In general, for a "k-row" flower, we have $1 + 6\binom{k}{2}$ hexagons. Obviously, this number will never be divisible by 6, but if we take our expression mod 7 we get $(k-2)(k+1) \equiv 0$ , so $k = 6$ will suffice.