The pulleys move
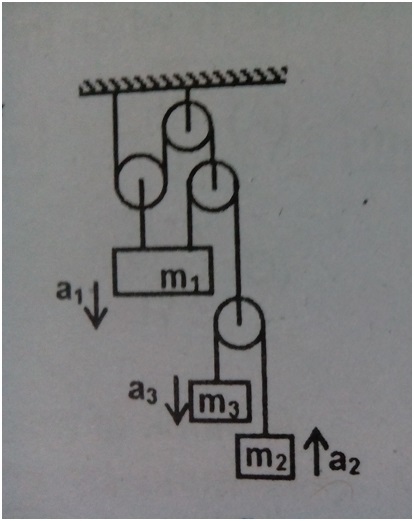 The pulley block system is shown in the figure. All strings and pulleys are ideal. The relation between
is given as
where
are co prime integers. Find
.
The pulley block system is shown in the figure. All strings and pulleys are ideal. The relation between
is given as
where
are co prime integers. Find
.
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
By the concept of virtual work method we get
∑ T a = 0
From the figure
− ( 2 T + 2 T ) a 1 − 4 T a 3 + 4 T a 2 = 0
So − 1 0 a 1 + a 2 − a 3 = 0
So ∣ x + y + z ∣ = 1 0