The Pyramid Scheme!
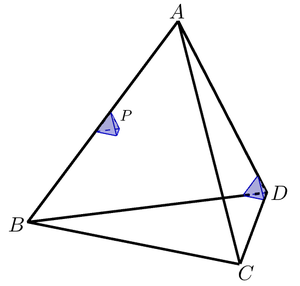
In the regular tetrahedron of edge length , there is the blue regular tetrahedron of edge length . As shown above, tetrahedron can move freely as long as it touches any edge of the tetrahedron . At this time, how many times the volume of the tetrahedron is the volume of the part through which the tetrahedron does not pass (inside the tetrahedron )?
Try to do this without any trigonometry.
The answer is 850.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
In order to calculate the volume of such a pyramid we need to know the length of its height.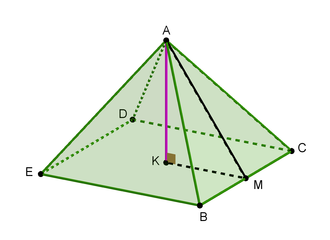 Figure 2
In figure 2, we have
K
M
=
2
1
,
A
M
=
2
3
, thus, by Pythagorean theorem,
A
K
=
A
M
2
−
K
M
2
=
(
2
3
)
2
−
(
2
1
)
2
=
2
1
Hence,
V
p
y
r
a
m
i
d
=
3
1
[
B
C
D
E
]
⋅
A
K
=
3
1
×
1
2
×
2
1
=
3
2
1
The volume of the part through which the tetrahedron
P
passes, is the compound volume of the 52 copies of
P
plus the volume of the pyramids. On every edge there are 9 of them, but the ones nearest to the vertices of
A
B
C
D
do overlap, producing a regular octahedron (two pyramids with common base) form which a part is not covered by moving
P
. This part corresponds to the polyhedron outlined with black edges in figure 3. Its volume is one fourth of the pyramid, hence, near every vertex of
A
B
C
D
we have a volume of
(
2
−
4
1
)
V
p
y
r
a
m
i
d
=
4
7
V
p
y
r
a
m
i
d
covered by moving
P
.
Figure 2
In figure 2, we have
K
M
=
2
1
,
A
M
=
2
3
, thus, by Pythagorean theorem,
A
K
=
A
M
2
−
K
M
2
=
(
2
3
)
2
−
(
2
1
)
2
=
2
1
Hence,
V
p
y
r
a
m
i
d
=
3
1
[
B
C
D
E
]
⋅
A
K
=
3
1
×
1
2
×
2
1
=
3
2
1
The volume of the part through which the tetrahedron
P
passes, is the compound volume of the 52 copies of
P
plus the volume of the pyramids. On every edge there are 9 of them, but the ones nearest to the vertices of
A
B
C
D
do overlap, producing a regular octahedron (two pyramids with common base) form which a part is not covered by moving
P
. This part corresponds to the polyhedron outlined with black edges in figure 3. Its volume is one fourth of the pyramid, hence, near every vertex of
A
B
C
D
we have a volume of
(
2
−
4
1
)
V
p
y
r
a
m
i
d
=
4
7
V
p
y
r
a
m
i
d
covered by moving
P
.
We denote by V ′ the volume of the part inside A B C D through which the tetrahedron P does not pass and by V P the volume of P .
The similarity ratio of A B C D and P is r = edge of P edge of A B C D = 1 0 , hence V ′ = r 3 V P ⇒ V ′ = 1 0 0 0 V P Doing the calculations for the required number, V p V ′ = V P V A B C D − { 5 2 V P + ( 6 × 7 + 4 × 4 7 ) V p y r a m i d } = V P 1 0 3 V P − ( 5 2 V P + 4 9 V p y r a m i d ) = 6 2 1 3 9 4 8 × 6 2 1 3 − 4 9 × 3 2 1 = 9 4 8 − 9 8 = 8 5 0 Thus, V ′ = 8 5 0 V P . The answer is 8 5 0 .