How Many Queens?
 How many queens can be placed on an
8
×
8
board such that no two queens are in the same row, column, or diagonal path?
How many queens can be placed on an
8
×
8
board such that no two queens are in the same row, column, or diagonal path?
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Hi dan! board you have made is 10 x 10 boeard
your solution was for 10x10 board not 8x8 board.
if not mistaken there's only 7 queens could be placed in 8x8 board.
Log in to reply
there is a youtube video by a channel numberphile on 8 queen problem
Yes, 8 is the correct answer. The problem of finding these arrangements of 8 queens that satisfy the problem's requirements is a very famous problem called the Eight Queens Problem . It is classical problem in CS and is generally taught as an introduction to recursion.
there's Queen in the same column
We can think about it using matrices. Queens are our pivot positions in an 8*8 matrix.
Just use the longest diagonal. Only a queen occupies that entire row and column.
Then the queens will be in diagonal path
Log in to reply
My bad. haven't noticed the diagonal in the question. thanks


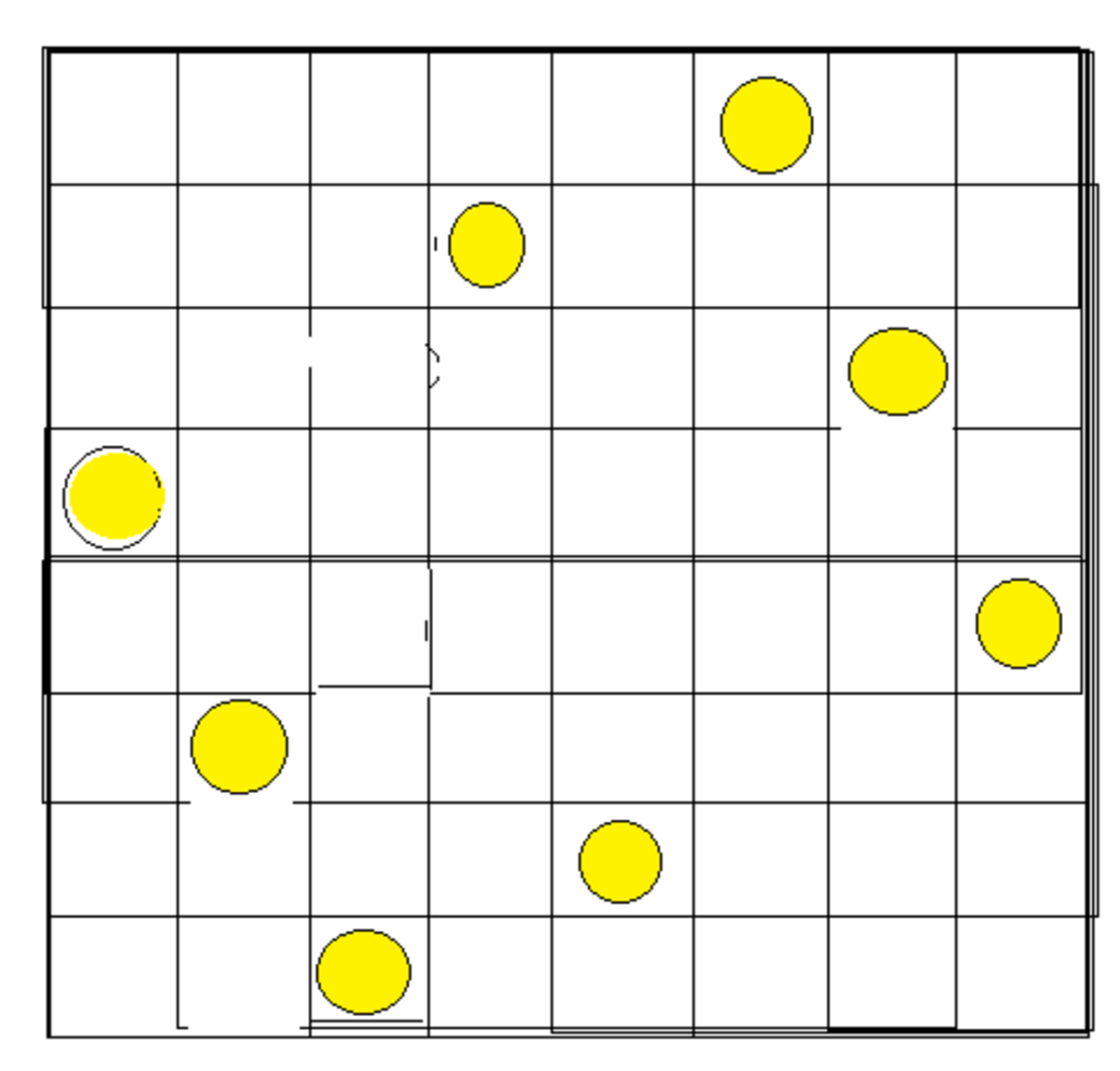
Since a queen's domain includes her entire row and column, each time we place a queen, there can be no more queens in either that row or that column. Thus, there is a maximum of 8 queens. To show that 8 queens is attainable, check out the following placement: