The rectangle stuck in the triangle

A rectangle is inscribed in a triangle as given in the figure below.

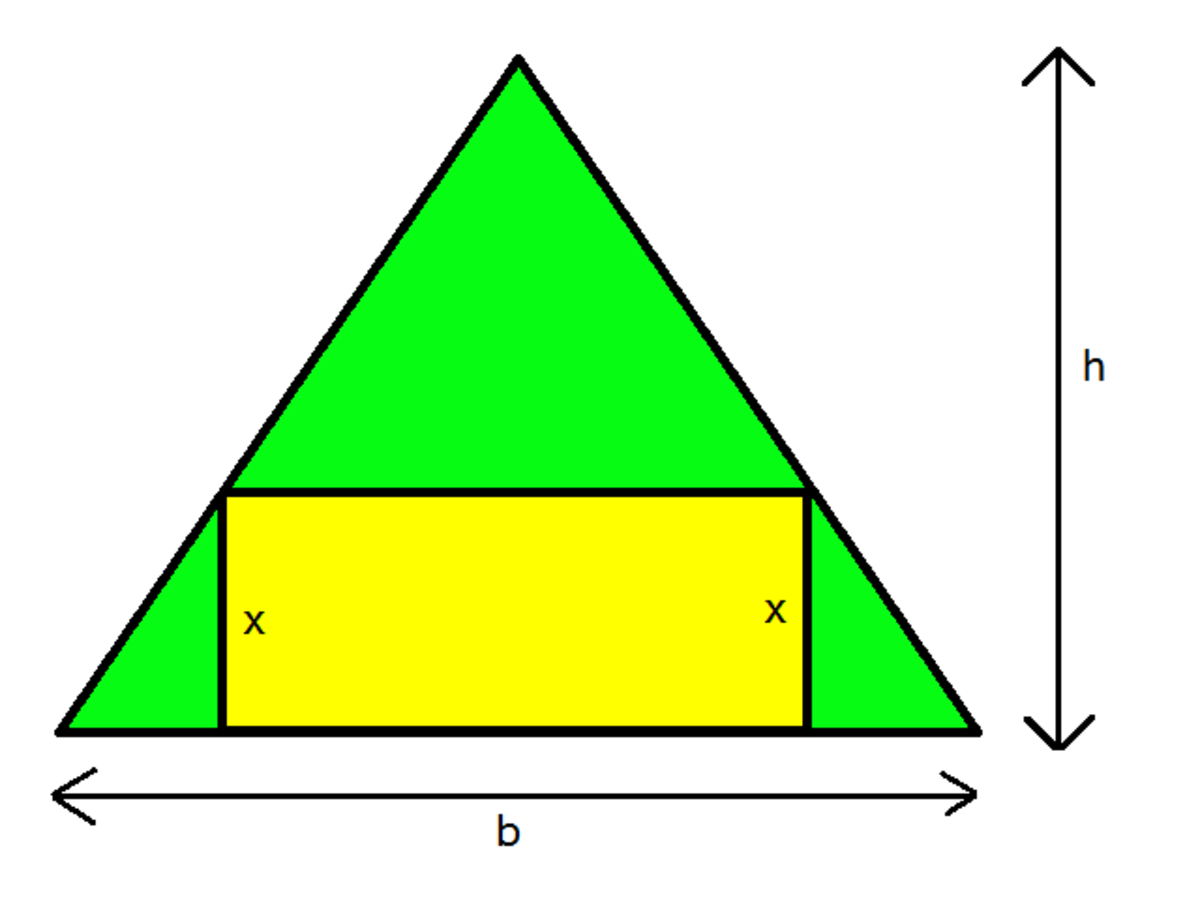
What is the perimeter of the rectangle in terms of $b$ , $h$ and $x$ ? In other words, what is the function $f(x)$ which gives an output equal to the perimeter of the inscribed rectangle when $x$ is plugged into it?

Note:

1. The triangle looks isosceles in the figure but that isn't necessarily true. The question only gives us information about the length of the base and height of the triangle.
2. $x$ is the length of those sides of the rectangle which are perpendicular to the base of the triangle.