The Red and Blue Friends
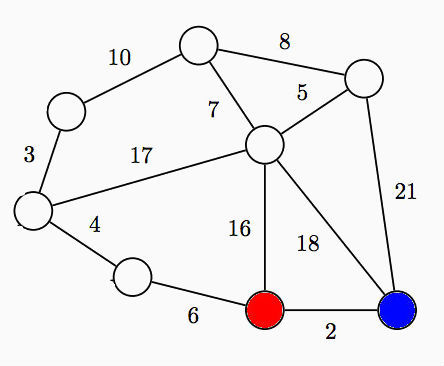The Map of the Empire
In Sheldor's empire, there are several villages connected by roads of different length. The map of the empire is shown above.
However, because the emperor cannot put up with the high costs of maintaining so many roads decided that he would only keep as many roads as to keep the whole kingdom connected but the total length of the roads is minimum. He would blow up all the other roads.
The direct road between and is the shortest road in the empire. Will this road still be kept in this regime?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5-7-10-3-4-6-2 is a solution of length 37. If 2 was not included in the shortest solution, then 18 or 21 would be needed in order to connect blue. Since you need at least 7 roads to connect 8 cities, that means you would need the 6 other roads to add up to at most 19 in order to be as short. Even if 3 was part of the solution, that would still require the remaining 5 roads to average less than 4, which is clearly impossible since none of the other roads are less than 4.