The required number
I'm thinking of a number.
- It is a two-digit positive integer.
- The sum of its digits is 10.
- Subtracting 72 from the number swaps its two digits.
What is the number?
The answer is 91.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
34 solutions
Is there a name for this type of problem, I want to learn more about them.
haha answer is 91 and 91% people got it right
Suppose the digit in unit's' place of the two digit number is x and the digit in tens' place is 1 0 − x
Now,
1 0 ( 1 0 − x ) + x = 1 0 0 − 9 x
According to the question,
( 1 0 0 − 9 x ) − 7 2 = 1 0 x + ( 1 1 0 − x ) ⟹ x = 1
Hence 1 0 0 − 9 = 9 1
110 should be 10, I think, in the next to the last line
Let the number be A B . Then the reverse would be B A . The number can be written as 1 0 A + B , and the reverse as 1 0 B + A . We can write two equations:
A + B = 1 0
1 0 A + B − 7 2 = 1 0 B + A ⟹ 9 A − 9 B = 7 2 ⟹ A − B = 8 .
Add these two equations to find that A = 9 , so B = 1 , and our answer is 9 1 .
When you posted your solution it was my birthday. I was shocked at the date.😨😨😨😨😨😨😨
It's like you have the same solution as the others.
Given that the sum of digits of two digit positive integer is 10, the possible pairs are (1,9), (2,8), (3,7), (4,6), (5,5).
Also given that subtracting 72 from the number swaps its two digits. Hence need to check the number 73, 82 and 91 (all other numbers are less then 72)
The number 73 and 82 not satisfies the required condition. The only number satisfying the given condition is 91. ( 91 -72= 19 )
That's how I worked it out
I like this solution the most because it is fast and can be done in your head.
js code to test in the browser console:
var nums = Array
.from( { length: 99 - 10 + 1 }, ( v, i ) => i + 10 )
.filter( v => ( +( "" + v )[ 0 ] + ( +( "" + v )[ 1 ] ) ) == 10 )
.map( v => [ v, v - 72 ] )
//JSON.stringify( nums )
// "[[19,-53],[28,-44],[37,-35],[46,-26],[55,-17],[64,-8],[73,1],[82,10],[91,19]]"
.filter( ( [ a, b ] ) => ( "" + a )[ 0 ] + ( "" + a )[ 1 ] == ( "" + b )[ 1 ] + ( "" + b )[ 0 ] );
nums;
// [91, 19]
The 2-digit numbers that the sum of their digits is 1 0 are:
9 1 / 1 9 , 8 2 / 2 8 , 7 3 / 3 7 etc.
We can eliminate all of the numbers except 9 1 , 8 2 and 7 3 for having a negative solution through subtracting 7 2 .
So with a quick check we can see the correct answer.
Dude it is quite easy. All you have to do is look at all of the 2 digit numbers above 72 that's digits add up to ten. There is 73, 82, or 91 as possibilities. Well 73 is out of the running because 73-72=1 and one is not 73 with it's digits swapped. That leaves 82 and 91. 82's reversed digits are 28. Since 82-72=10, 82 is out of the running as well. By default 91 has won. But, if you want to double check your answer, 91 with it's digits swapped is 19. 92-72=19. So 91 is for sure the answer.
72 can be subtracted either from 82 or 91, 82 minus 72 is 10 which doesn't fit for swap condition, 91 minus 72 is 19 , sum is equal to 10 even on swapping
Check out the 4 choices:
- 81 ⟹ Sum of digits is not 1 0 ⟹ F a l s e
- 36 ⟹ Sum of digits is not 1 0 ⟹ F a l s e
- 91 ⟹ Sum of digits is 1 0 ⟹ 91 - 72 = 19, hence reversed as is the second rule ∴ It is T r u e
There are no choices.
I think the question is rephrased. It did not have choices. So your answer is not relevant to the question.
Log in to reply
I think @Sakib Nazmus has edited it. it was there before
Let t be the tens' digit and u be the units' digit. Then the number is 1 0 t + u and the reversed number is 1 0 u + t . The equations are
t = 1 0 − u ( 1 )
1 0 t + u − 7 2 = 1 0 u + t ( 2 )
Solving for t in ( 1 ) and substituting in ( 2 ) , we have
1 0 ( 1 0 − u ) + u − 7 2 = 1 0 u + 1 0 − u
1 0 0 − 1 0 u + u − 7 2 = 1 0 u + 1 0 − u
1 8 = 1 8 u
u = 1
It follows that t = 1 0 − 1 = 9 . So the number is 9 1 .
x+y=10 (1) 10x+y -72=10y+x (2) Putting (1) in (2) gives 10x +10-x-72= 10(10-x) +x 9x-62=100-9x 18x=162 x=9 Therefore, from (1) we have y=1 Thus the no is 10x+y= (9*10)+1= 91
Suppose x is the unknown number, a its first digit and b its second digit. Then x = 1 0 a + b . We have that a + b = 1 0 , or equivalently, b = 1 0 − a . Also, 1 0 a + b − 7 2 = 1 0 b + a . Substituting b for 1 0 − a in the last equation and solving for a we get a = 9 . Then b = 1 0 − a = 1 and x = 9 1 .
I actually tried trial and error, possible numbers 91,82,73,64,55,46,37,28,19 where i can skip the numbers below 72. 91—72=19 works right away.
Let x = a b . We know that: a b − 7 2 = b a and that a + b = 1 0 . Thus, 1 0 a + b − 7 2 = 1 0 b + a ⟹ 9 a + a + b − 7 2 = 9 b + a + b ⟹ 9 a − 7 2 = 9 b We divide this relation by 9 , and we get: a − 8 = b ⟹ a = b + 8 . Plugging into our second equation, b + 8 + b = 1 0 , so b = 2 1 0 − 8 = 1 . Now, it is trivial to find a too: a = 1 0 − 1 = 9 .
So our x = a b = 9 1 .
There are 3 numbers higher than 72 that fit the first two rules: 73, 82 and 91. Substract 72 drom each to find 91 - 72 = 19; only 91 fits 3 rules.
Let the number be A B , where A and B are single-digit integers. Then we have:
{ A + B = 1 0 1 0 A + B − 7 2 = 1 0 B + A ⟹ A − B = 8 . . . ( 1 ) . . . ( 2 )
( 1 ) + ( 2 ) : 2 A = 1 8 ⟹ A = 9 ⟹ B = 1 ⟹ A B = 9 1 .
I will let the number x . Then, the last digit will be let b and the other digit will be a . Then x = 1 0 a + b . We can let a simultaneous equation like this. a + b = 1 0 1 0 a + b − 7 2 = 1 0 b + a . The answer of a =9, b =1. So x is 91.
When I solved it, it was '91% of people got this right'!!!
Let the number be xy i.e. 10x + y
So, according to question,
Number - 72 = Reversed Number
=> (10x + y) - 72 = (10y + x)
=> x - y = 8
Also, Sum of digits = 10
=> x + y = 10
And, on solving (1) & (2), we get x = 9, y =1
Hence, the number is 91
How I did this problem simply by listing all the sums, 1+9=10 and (using place value logic) 10+9=19 and the rest of the sums, 28, 37 etc. You cannot use anything below 72 or else it will become a negative (e.g. 19-72=-53) How you get the solution is if you got the sum before hand and if you reverse it. It has the same sum so 1+9=10 9+1=10. So the answer is 91. It will ALWAYS be the FIRST sum that you reverse (sorry if it's not algebra this is just the most simple answer.) :D
We know that the number is larger than 72. This leaves three candidates, 73, 82 and 91. Check all of them.
Let the digits be x and y. Let the number be 10x+y as in 25=20+5. So x+y =10 as eqn 1 and 10x+y-72=10y+x. Substitute y =x-10 into eqn 2 and your ans will be 9 put bavk in eqn one to get y as 1 so your number is 91 .To confirm 91-72=19
Although this can be solved algebraically, it is easier to test the three possible positive two digit-positive numbers higher than 72: 73, 82, and 91. 73-72= 1; 82-72= 10; 91-72= 19. The answer must be 91.
Let's see hmmm...yeah ummm... 6+4 is 10 but 64-72 is not 46 so we need a bigger number..how about 9+1.... Perfect!!!
We write all possibilities for 2 digit number the sum of them is 10 And the number is greater than 72 So we have 91 73
Then we try each one 91-72= 19
We have the right answer !
I tried all the combinations where a + b = 10
1+9
2+8
3+7
4+6
5+5
6+4
7+3
8+2
9+1 (solution)
First off this number must be positive, which means it has to be greater than 72. That means we are left with 3 numbers, 73, 82, and 91. The only number that has its digits flipped after subtracting 72 is 91, so 91 is our answer.
From the 9 possible numbers with sum of digits 10, we drop 19, 28, 37, 46, 55 and 64 because we cannot subtract 72. From the remaining 3 numbers: 73, 82 and 91, only 91 works.
These are the possible 2-digit numbers, with the sum of their digits equal to 10.
- 19
- 91
- 28
- 82
- 37
- 73
- 46
- 64
- 55
Starting from the largest number which is 91, try subtracting 72 and we get 19. so it is the correct one
I found my answer solely based on the line that says 'the sum of its digits is 10'.
9+1 = 10. One condition verified. Now let's subtract 72 from 91. It's 19. So 91 is the number we are looking for.
No need for equations and such.
By the way, if you think about it logically, it becomes impossible once you get to 6+4 (64) because subtracting 72 from that number would give a negative result. So it narrows down to 9+1, 8+2 and 7+3 only. That's it.
You can solve it by simply mentally juggling the numbers > 72 to 99
numbers are swapped, therefore not 55, and greater than 72, only choices were 73, 82 and 91.73-72=01=X, 82-72=10=X, thus 91
Similar problem: - I'm thinking of a two digit positive number - Subtracting 72 from this number equals the sum of its digits
What is the number?
It is 8 1
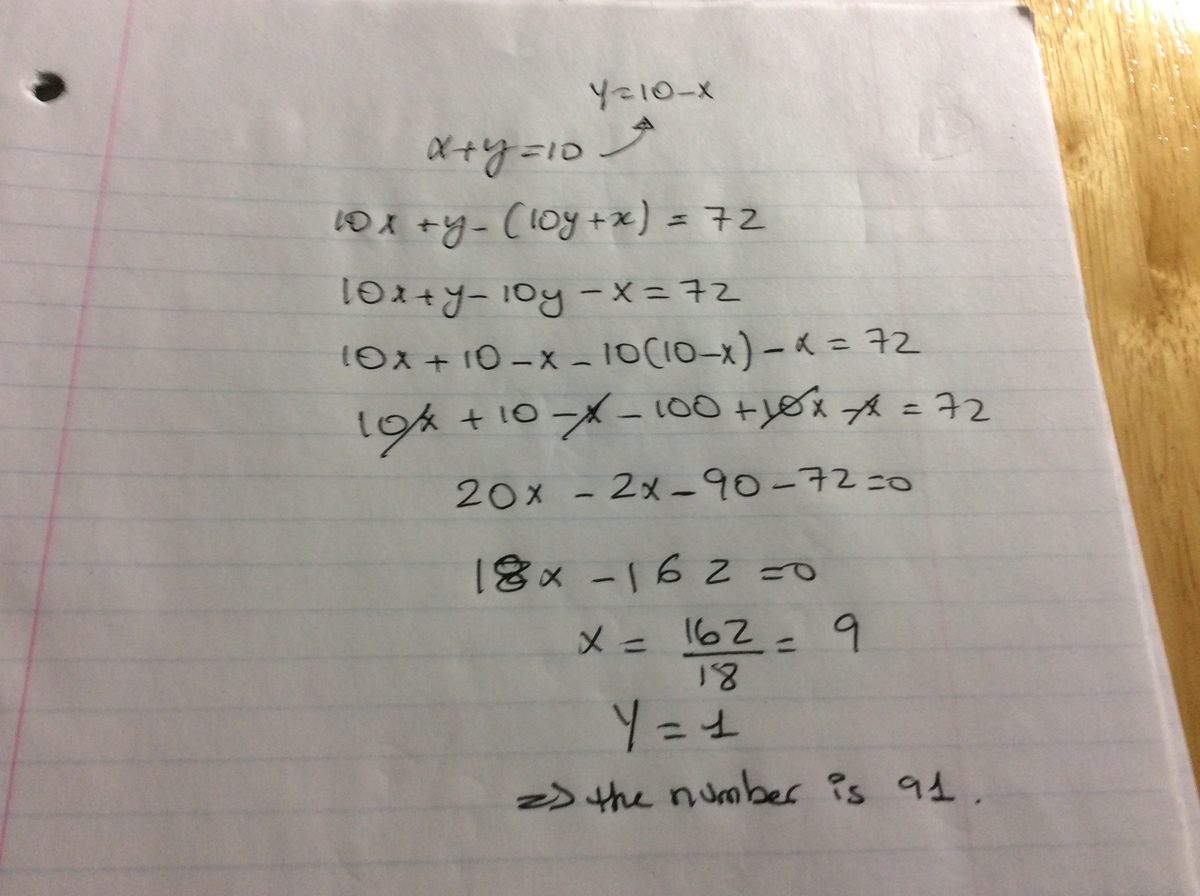
Let our number be a b = 1 0 a + b , when the digits are reversed the number becomes b a = 1 0 b + a .
By the above statements, a + b = 1 0 and 1 0 a + b − 7 2 = 1 0 b + a .
Solving the two equations we get a = 9 , b = 1 . Thus our number is 9 1