the right-down traveller
In how many ways can you travel from the left top corner to the right bottom corner of an M X N grid where M = 30 and N = 20 with the following constraints ( believe me. these constraints make the problem more easy :-) )?
- Traveling is allowed only on the borders of the squares.
- You can travel only rightwards or downwards.
Note: M is the number of rows. N is the number of columns. an M X N grid contains M*N squares.
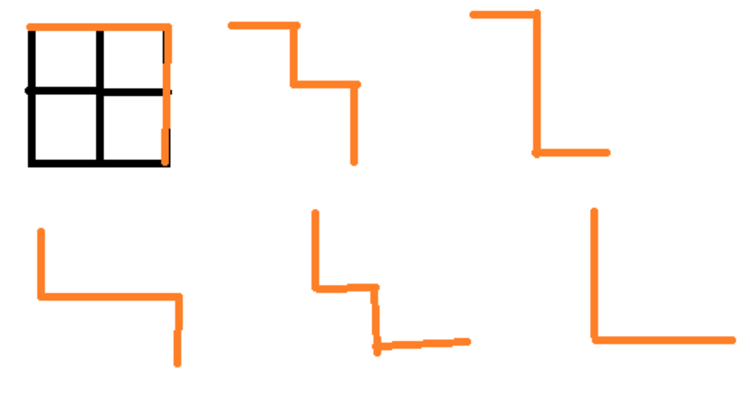
For example: a 2X2 grid, we have 6 ways to traverse as given in the illustration.
(Sorry for the shabby illustration. I am a really impatient guy :-P)
The answer is 47129212243960.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
always observe that traversing can be done only leftwards and rightwards. now for a 2X2 grid, possible ways are: LLDD LDLD LDDL DLLD DLDL DDLL
where D: down, L: left Hence the solution is the number of ways how you can put two L in 4 places. i.e., 4C2.
Hence for an MXN grid, the solution would be (M+N)CN or (M+N)CM
Hence answer is (20+30)C20 = 50C20 = 47129212243960.