The Right Kite
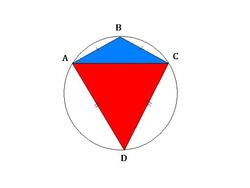 Diagram above shows a kite
A
B
C
D
circumscribed in a circle.
Diagram above shows a kite
A
B
C
D
circumscribed in a circle.
If the area ratio of the red to the blue region is 3 : 1 , what is the measure of ∠ A B C in degrees?
Hint : If you know the right kite, things will get much easier.
The answer is 120.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Impressive solution
would you plz show me how is "BP=OP" ??
Log in to reply
O P = O B − B P = r − 2 1 r = 2 1 r = B P
Let ∠ A B C = θ , A B = B C = b and A D = C D = r . We know that ∠ A B C + ∠ A D C = 1 8 0 ∘ because A B C D is cyclic, hence ∠ A D C = 1 8 0 ∘ − θ . Also [ A D C ] = 3 [ A B C ] . Using Law of Sines to compute the area we get: r 2 sin ( 1 8 0 ∘ − θ ) / 2 = 3 b 2 sin ( θ ) / 2 , which implies r 2 = 3 b 2 or b r = 3 .
Now, note that A C = 2 r sin ( 2 1 8 0 ∘ − θ ) and A C = 2 b sin ( 2 θ ) . Then: r cos ( 2 θ ) = b sin ( 2 θ ) .
Finally, we have b r = tan ( 2 θ ) , which is 3 = tan ( 2 θ ) and θ = 1 2 0 ∘ .
Let A C ∩ B D = E , Δ B E C ∾ Δ C E D ⇒ C E B E = E D E C ⇒ E D B E = ( E D E C ) 2
And I have, E D B E = a r e a ( r e d ) a r e a ( b l u e ) = 3 1 ⇒ ( E D E C ) 2 = 3 1 ⇒ E D 2 E C 2 + E D 2 = 3 4 ⇒ E D 2 D C 2 = 3 4 ⇒ cos E D C = 2 3 ⇒ ∠ A B C = 1 2 0 o
I will just outline my solution... It's quite easy to show that BD is a diameter. Therefore, angle BAD = angle BCD = 90. Let E be the intersection of the diameter BD and the line AC. Using the ratio 3:1 provided, it follows that BE = BD/4 and DE = 3BD/4. Let F be the center of the circumference. Draw the triangle AFC. Can you see that this triangle and the triangle ABC are congruent? Yes, they are! Therefore, angle ABC = angle AFC. Moreover, AFC = 2ADC. Since ABC + ADC = 180 and ABC = AFC, ABC = 2ADC. Finally, ABC + ABC/2 = 180 and angle ABC = 120.
Yes, that's why it's called the right kite because it's got 2 right angles. Great job!
Since the triangles have same base but 1:3 areas, their heights must be 1:3. The half way point of the combined altitude (the diameter) is the center, But it divides the red altitude in 1:2 (the centroid!) So the red triangle must be equilateral, making the desired angle 180-60 = 120. Because the two triangles together form a cyclic quadrilateral.
Let the center of the circumcircle be O and its radius be r , and B O cuts A C at P .
Since the ratio of areas: ∣ △ A D C ∣ ∣ △ A B C ∣ = 3 1 ⇒ B P = O P = 2 1 r ⇒ D P = 2 3 r .
We see that cos ∠ C O P = O C O P = r 2 1 r = 2 1 ⇒ ∠ C O P = 6 0 ∘ ⇒ C P = 2 3 r .
Therefore, tan ∠ C B P = B P C P = 2 1 r 2 3 r = 3 ⇒ ∠ C B P = 6 0 ∘ ⇒ ∠ A B C = 2 × ∠ C B P = 1 2 0 ∘