The Right Side of Lightning
I captured a snapshot of lightning as it hit the ground. What is the sum of all 15 marked angles?
Assume that the base of the cloud and the ground to be parallel lines.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Moderator note:
The general idea of adding line segments to make a larger geometric figure is helpful in an enormous number of cases and should always be considered if a geometry problem is causing difficulty.
Isn´t the (n-2) x 180º rule exclusive for convex polygons?
Log in to reply
The formula is based on the fact that you can divide a n-sided polygon into
n
−
2
triangles. You can do this whether the polygon is convex or not. The formula is often used for convex polygons, but its validity is not restricted to them.
Nice solution! I solved it by rotating a pencil along the lines of the lightning. I counted that the pencil made 7 full turns, so the sum of angles is 7 × 3 6 0 ∘ = 1 4 × 1 8 0 ∘ = 2 5 2 0 ∘ .
Log in to reply
Very Intuitive Approach. I revolved my mobile screen as the lightning streak bent and counted the number of full rotations😂.
17 minus 2 doesn't equal 14...
Log in to reply
Yes, ( 1 7 − 2 ) × 1 8 0 ∘ is 1 5 × 1 8 0 ∘ . There is another step in between: Marta has subtracted the two right angles (in the left part of the diagram), so the sum of desired angles is ( 1 5 − 1 ) × 1 8 0 ∘ = 1 4 × 1 8 0 ∘ .
The triangle method to calculate interior angel sums on convex polygons also works on concave polygons.
Log in to reply
Yes, and it is quite clear from the picture that this lightning encloses a concave polygon.
a small correction...in the last line of the answer i should be (n-2) x 180
Log in to reply
Not really, the OP is counting the number of line segments in the lightning, not the polygon
I love it! This is a proof positive that all those people who gave up shouldn't have. They all had the knowledge base to do this, if they just put their mind to it.
Log in to reply
Yes, this problem is indeed very accessible to most of us.
Ohhh, a nice "proof without words" solution. My favorite solution here~!
Nothing new to be added.. simply by completing the polygon and applying n * 2 - 4 Rt angles.
Completing the polygon will give you 15-sided figure. If you only applied the formula ( 2 n − 4 ) × 9 0 ∘ = ( n − 2 ) × 1 8 0 ∘ you would get ( 1 5 − 2 ) × 1 8 0 ∘ = 1 3 × 1 8 0 ∘ not 1 4 × 1 8 0 ∘ as required. So I am assuming that you also added 1 8 0 ∘ somehow somewhere to make up what was cut off by completing the polygon. I am not sure how easy it would be to explain/justify the exact figure for that.
Also, even if that were done well, using some theorem about parallel lines, then your procedure would only work in certain cases. It creates a self-intersecting polygon. That means that the formula for the sum of internal angles is not guaranteed to work. Check out my "Crazy Lightening" for an example where it does not.
Log in to reply
I checked out your problem. It is a cool one.
Drop an altitude from point A to the ground, where A is the intersection point of the lightning bolt and the base of the cloud.
The boundary of the region enclosed by the altitude, lightening bolt, and ground determines a closed polygon with 16 sides.
The sum of the angles in this polygon is (16-2)*180 which corresponds to the sum of the angles in the diagram.
Log in to reply
True enough. But the reason your procedure comes up with the right figure is because one 9 0 ∘ angle was subtracted at the top, since your 16-sided polygon does not enclose all of the angles we are adding up, and another 9 0 ∘ angle was added at the bottom.
The lightening did happened to go far enough to the right far for your operation not to generate a self-intersecting polygon. Maybe I should have made it misbehave a bit more.
You can also use the rule that sum of complementary angles between 2 parallel lines is always 180. You can draw 2 parallel lines at the 2 ends of each line segment. Hence total sum of all angles = no. of line segments * 180
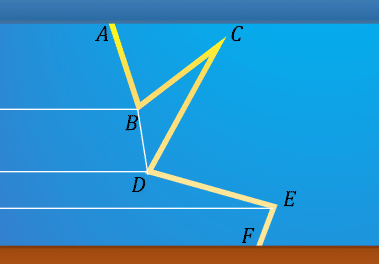
This would work beautifully if all of the segments continued on a downward journey toward the ground. Like this:
But if some go back up, as it the case in this instance:
triangles need to be introduced and things get complicated rapidly.
If you do not introduce triangles, the lines your are drawing are no longer in any definite relationship to the angles you are trying to calculate. The angles no longer go to the lines as they do in the simple case at the start of this comment.
Log in to reply
@Marta Reece the solution was specific to the given question. Although, even in the second diagram you have presented, it is possible to get the answer in similar way, but cannot be generalised. For instance, one can still draw parallel lines at the ends of each segment, but there will be a part of obtuse angle B which will be left out so one will have to add another 180 because of that. So, for each different figure we will have to check if such left-out angles are there.
And thanks a lot for the first figure. Clearly illustrates what I was trying to put in words.
Log in to reply
I boldfaced above what I believe is the core problem with your attempt at a solution.
Drawing parallel lines at the end of each line segment? Are you sure that's doable? I don't see any way of constructing these lines. Am I mistaken?
Log in to reply
Of course it is doable. Look at the first figure in Martha Reece' reply
The way I tried to solve this was by building up from a small case, and working my way up to a general technique. I started by trying to solve if there were only two line segments in the lightning. I did not use the polygon method that many other people did, but instead drew lines parallel to the ground through each bend in the lightning. Then the sum of the three angles could be found by obtaining the sum of the each of the "split" angles (the ones formed by drawing the parallel line) and the closest non-adjacent angle. To do this, you can use the theorem which states that the same-side angles formed by two parallel lines and their transversal are supplementary (sum to 180 degrees). In the small case of of two lightning segments, there are two pairs of same-side angles, so the sum of all angles would be 2(180). This technique can be generalized to say that in these types of problems where you have a lightning bolt made of s segments, the sum of the angles is 180 s . in tis problem, there are 14 line segments, so the answer is 14(180).
This works well for a well behaved lightening such as the one below.
But if any of the segments start going up, some triangles and the sum of their angles have to be introduced, and things get a lot more complicated very rapidly. An easy case can be seen below.
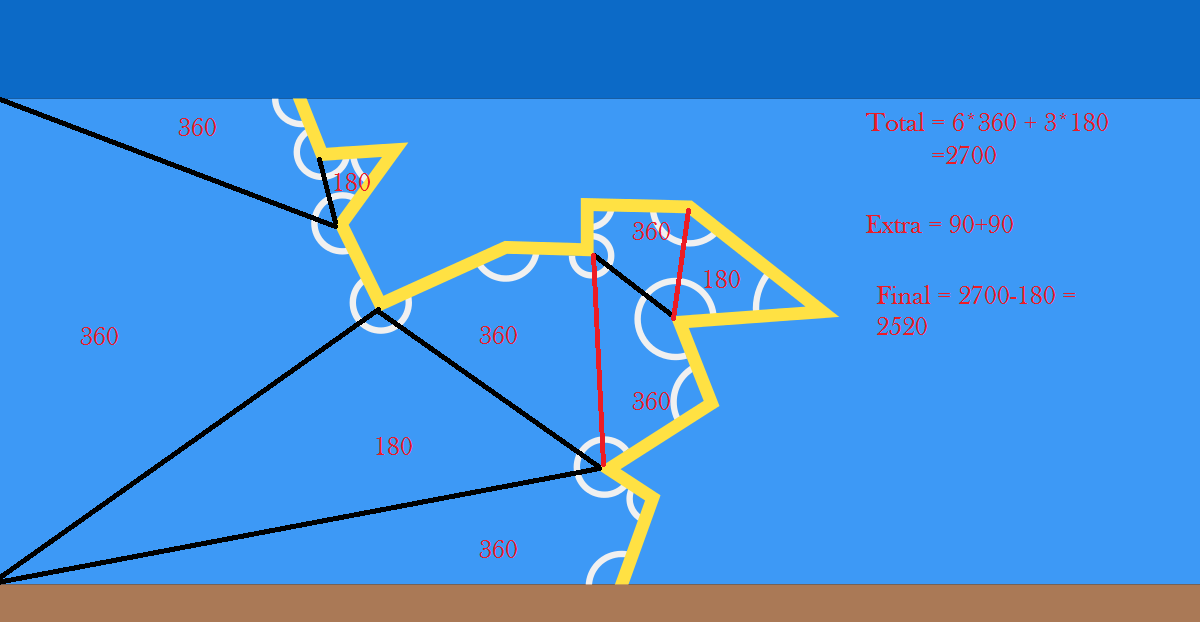
The line of the lightening together the three white lines form a 17-sided polygon with the sum of internal angles ( 1 7 − 2 ) × 1 8 0 ∘ . Subtract the two right angles which are not part of the desired sum, and we get 1 4 × 1 8 0 ∘ = 2 5 2 0 ∘ . Interestingly enough the line of the lightening has 1 4 segments. If there were n segments, the sum of the angles would be n × 1 8 0 ∘ .