The Right Time
Geometry
Level
2
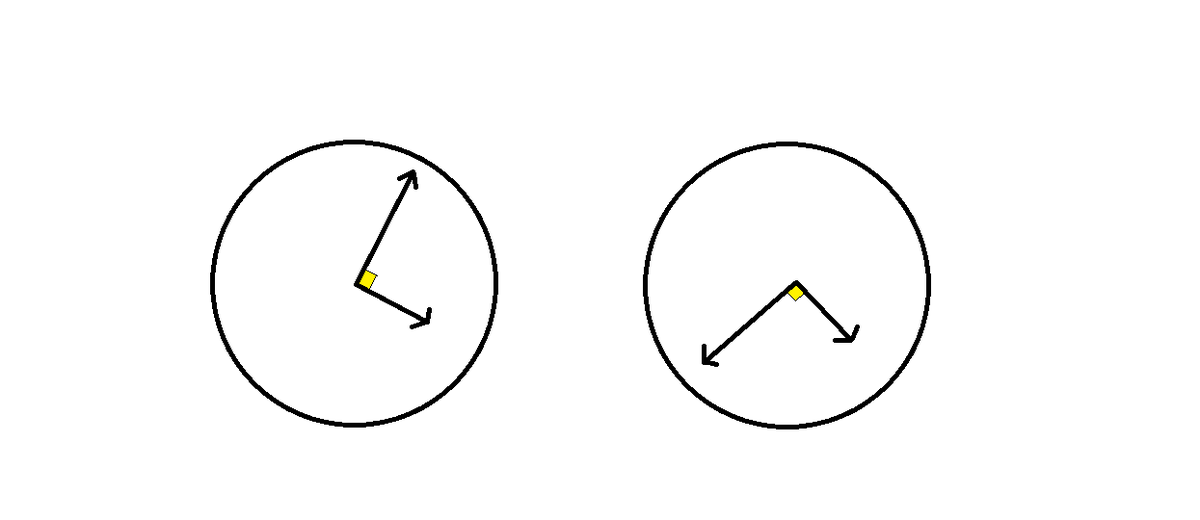
During each hour, the clock hands will always make a right angle twice as shown above.
Will the time gap between these 2 instances be constant for every hour?
No
Yes
Not enough information
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
The minute hand will move 6 3 6 0 = 6 degrees clockwise every minute while the hour hand will move 6 0 3 0 = 0 . 5 degree, for each hour only accounts for 1 2 3 6 0 = 3 0 degrees. Thus, each minute the angle between these hands will decrease by 6 − 0 . 5 = 5 . 5 degrees.
Once the hands make the first right angle, they will continue to move closer to each other until they are superimposed (making 0 degrees) and will start to form increasing angle of constant rate to eventually make a second right angle.
In other words, the time gap between these right angles equal 5 . 5 9 0 + 9 0 = 1 1 3 6 0 ≈ 3 3 minutes for every hour.