The right triangle that just got up and left

Let the two legs of the triangle have lengths $a$ and $b$ . Then the hypotenuse has length $\sqrt{a^{2} + b^{2}}$ , and the area can be expressed as both $\dfrac{1}{2}ab$ and as one-half the product of the length of the hypotenuse and the altitude to it, i.e., $\dfrac{1}{2}\sqrt{a^{2} + b^{2}}*12 = 6\sqrt{a^{2} + b^{2}}$ . Equating these two area expressions yields that $ab = 12\sqrt{a^{2} + b^{2}}$ .

Now the perimeter is $a + b + \sqrt{a^{2} + b^{2}} = 60$ , and so

$a + b = 60 - \sqrt{a^{2} + b^{2}} \Longrightarrow a^{2} + 2ab + b^{2} = 3600 + (a^{2} + b^{2}) - 120\sqrt{a^{2} + b^{2}}$

$\Longrightarrow 2ab + 120\sqrt{a^{2} + b^{2}} = 3600 \Longrightarrow 2*12\sqrt{a^{2} + b^{2}} + 120\sqrt{a^{2} + b^{2}} = 3600$

$\Longrightarrow 144\sqrt{a^{2} + b^{2}} = 3600 \Longrightarrow \sqrt{a^{2} + b^{2}} = 25.$

Thus $a + b = 60 - 25 = \boxed{35}$ .

(Note that as $ab = 12*25 = 300 \Longrightarrow b = \dfrac{300}{a}$ we have that

$a + \dfrac{300}{a} = 35 \Longrightarrow a^{2} - 35a + 300 = (a - 15)(a - 20) = 0$ ,

and so the two legs have lengths $15$ and $20$ .)

Let's call the hypotenuse H and the sum of the other two sides S. It is this $S=a+b$ which we want to find.

From the information on the perimeter we can see that

$S+H=60 \dots(1)$

Now let's work out the area of the triangle in two ways. We can take the hypotenuse to be the base and then the height is 12, or we can take the base to b and the height to be a. The area must come out to be the same in both cases, so we get (cancelling the factor of $\frac{1}{2}$ )

$ab=12H \dots (2)$

Now let us find the square of our desired quantity, and simplify it using Pythagoras's theorem

$S^2=(a+b)^2=a^2+b^2+2ab=H^2+2ab$

Now using equations (1) and (2) we can write this as

$S^2=(60-S)^2+24(60-S)$

When you expand the square bracket on the right hand side the terms in $S^2$ conveniently cancel to leave an easy linear equation to find

$\boxed{S=35}$

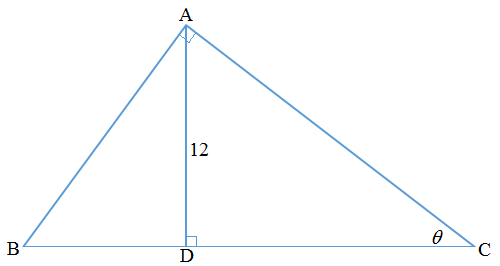
Let the right triangle described be $ABC$ , with $BC$ be the hypotenuse and $AD$ the altitude to $BC$ . Let the length of $BC=x$ and the smallest angle $\angle ACB = \theta$ . Then

$\begin{aligned} AB + BC + CA & = 60 \\ x \sin \theta + x + x \cos \theta & = 60 \\ x \left(1 + \sin \theta + \cos \theta \right) & = 60 & ...(1) \end{aligned}$

Consider $\triangle ACD$ , we note that

$\begin{aligned} CA \cos \theta & = AD \\ x \sin \theta \cos \theta & = 12 \\ \implies x & = \frac {12}{\sin \theta \cos \theta} & ...(2) \end{aligned}$

Substituting in $(1)$ ,

$\begin{aligned} \frac {12}{\sin \theta \cos \theta} (1+\sin \theta + \cos \theta) & = 60 \\ \sin \theta + \cos \theta & = 5 \sin \theta \cos \theta - 1 & \small \color{#3D99F6} \text{Squaring both sides} \\ \sin^2 \theta + 2 \sin \theta \cos \theta + \cos^2 \theta & = 25 \sin^2 \theta \cos^2 \theta - 10 \sin \theta \cos \theta + 1 \\ 25 \sin^2 \theta \cos^2 \theta - 12 \sin \theta \cos \theta & = 0 \\ \sin (2\theta) \left(\frac {25}4 \sin (2\theta) - 6\right) & = 0 \\ \implies \color{#3D99F6} \sin (2 \theta) & = \frac {24}{25} & \small \color{#3D99F6} \text{Since }\sin (2\theta) > 0 \\ \color{#3D99F6} \frac {2\tan \theta}{1+\tan^2 \theta} & = \frac {24}{25} & \small \color{#3D99F6} \text{Using the half-angle tangent substitution} \\ 12 \tan^2 \theta - 25 \tan \theta + 12 & = 0 \\ (4\tan \theta - 3)(3\tan \theta - 4) & = 0 \\ \implies \tan \theta & = \frac 34 & \small \color{#3D99F6} \text{Since }\theta \text{ is the smallest angle.} \end{aligned}$

Implying that $\sin \theta = \frac 35$ and $\cos \theta = \frac 45$ . Now the sum of lengths of the two legs $AB + CA$ $= \dfrac {12}{\cos \theta} + \dfrac {12}{\sin \theta}$ $= 15 + 20 = \boxed{35}$ .

Let $\triangle ABC$ be right at vertex $B$ . Let $\theta = \angle C$ . Then

$c = b \sin \theta$ and $a = b \cos \theta$ . Further, the altitude $h$ onto the the hypotenuse $b$ is given by

$h = 12 = a \sin \theta = b \sin \theta \cos \theta \hspace{12pt} (1)$

Now, the perimeter is $60$ , so

$b (1 + \cos \theta + \sin \theta ) = 60 \hspace{12pt} (2)$

Pluggin equation (1) into (2), and simplifying and re-arranging , we get

$(1 + \cos \theta + \sin \theta ) = 5 \sin \theta \cos \theta \hspace{12pt} (3)$

Noting that $\cos \theta + \sin \theta = \sqrt{2} \cos( \theta - \frac{\pi}{4} )$ and that,

$\sin \theta \cos \theta = \frac{1}{2} \sin(2 \theta) = \frac{1}{2} \cos( 2 (\theta - \frac{\pi}{4} ) )$ , equation (3) becomes,

$1 + \sqrt{2} \cos v = \frac{5}{2} \cos 2 v = \frac{5}{2} (2 \cos^2 v - 1 ) \hspace{12pt} (4)$

where $v = \theta - \frac{\pi}{4}$ . Simplifying equation (4), one obtains,

$10 \cos^2 v - 2 \sqrt{2} \cos v - 7 = 0$

Solving using the quadratic formula,

$\cos v = \frac{1}{20} ( 2 \sqrt{2} \pm \sqrt{ 288 } ) = \frac{1}{10} ( \sqrt{2} \pm 6 \sqrt{2} )$

So that, the two possible values of $\cos v$ are $\frac{7}{10} \sqrt{2}$ and $- \dfrac{1}{\sqrt{2} }$ .

By inspection, the second of these values is extraneous and can be safely ignored. This leaves the first value of $\frac{7}{10} \sqrt{2}$ .

There are two values for the angle $v$ with this cosine. Using a standard scientific calculator, these two values are $v = 8.1301023541^{\circ}$

and $v = - 8.1301023541^{\circ}$ . This implies that the two values of $\theta$ are $\theta = 45^{\circ} - 8.1301023541^{\circ} = 36.8698976459^{\circ}$

and $\theta = 45^{\circ} + 8.1301023541^{\circ} = 53.1301023541^{\circ}$ . These are the two possible values for the angle $\theta$ , and as can be seen they are

complementary. These famous angels have the values for the sine and cosine of $\frac{3}{5}$ and $\frac{4}{5}$ and vice-versa.

Now we're ready to calculate the hypotenuse, $b = \dfrac{12}{\sin \theta \cos \theta } = 25$ .

Hence, $a + c = b ( \cos \theta + \sin \theta ) = 25 ( \frac{3}{5} + \frac{4}{5} )= \boxed{35}$ .

Let the sides of the triangle are a,b, and 60 – (a+b) Pythagoras law : a^2+ b^2= [60 – (a+b)]^2, ab – 60(a+b) + 1800 = 0, By similarity: b/12 = [60 –(a+b)]/a, ab = 12[60 – (a+b)], Substitute ab,to the first equation, a+b = 35.

area is given by(1/2)ab and (1/2)(12)(c), so ab = 12c. . Since P = 60, a + b = 60 -c. Squaring, a^2 + 2ab + b^2 = 3600 - 120c + c^2.. Substituting 2ab = 24c, and from the Pythagorean Theorem, a^2 + b^2 = c^2, we have: a^2 + b^2 = 3600 - 144c + c^2, or c^2 = 3600 - 144c + c^2, and 144c = 3600, c = 25. Then a + b = 60 - c =35.

The hypothenusa is the diameter of a circle that circumscribes the triangle:

2R cos(t) + 2R sin(t) + 2R = 60

2R cos(t)sin(t) = 12

squaring the first and combining the two equations gives R = 25/2

sin(2t) = 2sin(t)cos(t) = 24/25

I determined t from that and A+B = 2R (cos(t) + sin( t)) = 35

"Since P=60, the perimeter of this right triangle is an integer, the sides must also be integral."
Above was the bases of my solution. It is a wrong assumption. so I have deleted my solution.
Thanks to Brian Charlesworth . See his comment given below. [link text]