The Ring is retarded to 0 rad/s
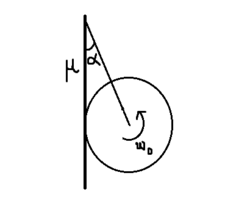 Consider a ring of mass
and radius
touching a rough wall of coefficient of friction
as shown in figure. The ring has an initial angular velocity of
.
Consider a ring of mass
and radius
touching a rough wall of coefficient of friction
as shown in figure. The ring has an initial angular velocity of
.
Find the time taken by the ring to come to a halt.
Details and Assumptions
-
The ring doesn't translate on the wall.
-
-
-
-
-
-
Try my set
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Since the ring does not translate on the wall, let us consider translational equilibrium.
∑ F x = ∑ F y = 0
Let the frictional force by the wall on the ring be f , Normal reaction be N and Tension is the string be T .
∑ F x = N − T sin α = 0
∑ F y = f + T cos α − m g = 0
f = μ N
Now the Rotational motion is to be analysed. The Friction would give angular retardation, say β (since α is used) about the centre of the ring.
Writing Torque equation about centre of ring,
f R = m R 2 β
To find time taken to retard to 0 r a d / s :
0 − ω 0 = − β t ⇒ t = β ω 0
Solving these equations, you get
f = μ sin α + cos α μ m g sin α
β = ( μ sin α + cos α ) R μ g sin α
t = μ g sin α ω 0 ( μ sin α + cos α ) R = 2