The River Crossing

Here is the diagram which visualizes the given question :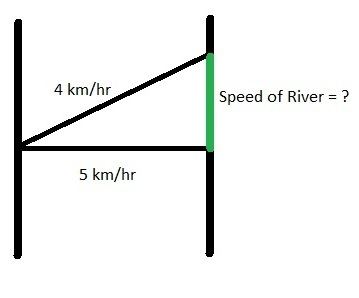

The $\color{#20A900}\text{green line}$ shows the velocity of the river. The velocity of the boat while crossing river (4 km/hr) and the velocity of the river are the given vectors to which the speed of boat in still water (5 km/hr) is the resultant vector. Let the velocity of water be $a$ .

$ai + 4j = 5$

$\implies \sqrt{a^2 + 16} = 25$

$\implies a = \sqrt{25 - 16} = \sqrt{9} = \pm 3$

Since speed cannot be negative the speed of river is $3 km/hr$

The boat crossing speed is a resultant of still water speed and river velocity. Imagining this as a vector should solve the problem. We have still water speed (SPS)and boat final crossing speed(BFCS). BFCS will be naturally perpendicular to river velocity. The result will be a right-angled triangle.We know the hypotenuse = 5 and one of the arms of the triangle = 4. Using the Pythagorean Theorem, we will find the other arm = 3,because 5^2= 4^2 + x^2 = 25=16+y=25=16+9= river velocity=3 km/h.