The Rubber Band Ant Problem
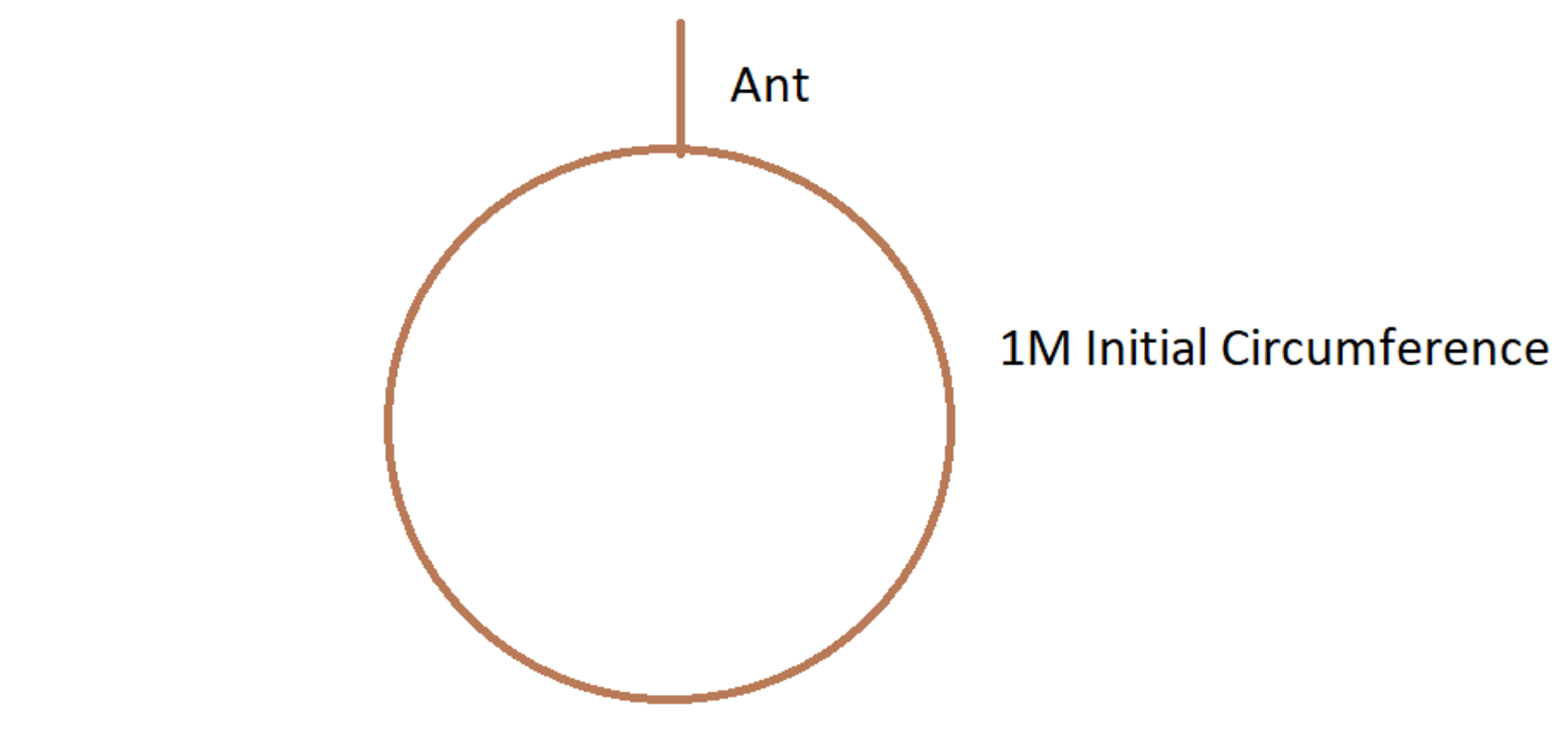
An ant begins its journey at the top of a 1m long rubber band. Traveling at a constant speed of 1cm/s, it begins to walk around the entire rubber band. However, every second, after the ant has moved, the rubber band is stretched out a further 1m in all directions. Assume the rubber band is perfectly circular and is stretched equally in all directions. Will the ant ever be able to complete a full revolution of the rubber band?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
At first, It may seem like this is a logic puzzle not a number theory puzzle. However, this question is closely related to the Harmonic Series. It seems that the ant will never make it around the rubber band, every time it gets closer, it gets pushed away. However, when a circle is enlarged, it is enlarged equally in all direction.Therefor, As the length of rubber band in front of the ant increases, the length of rubber band behind it increased as well. As a result the percentage of the rubber band traversed will remain constant. Initially, the ant traverses 1cm of the 1m rubber band. After it is stretched it has traveled a relative 1% of the rubber band. After traveling 2cm of the 2m the ant has traveled an additional 0.5% of the rubber band. This pattern continues on giving you the following series. - 1 + 1 / 2 + 1 / 3 + 1 / 4 + … + 1 / n This is known as the Harmonic series and is Divergent. We can approximate the time it will take for an entire revolution to be e 1 0 0 .
Inspired by Numberphile