The same as ∠ F A C ?
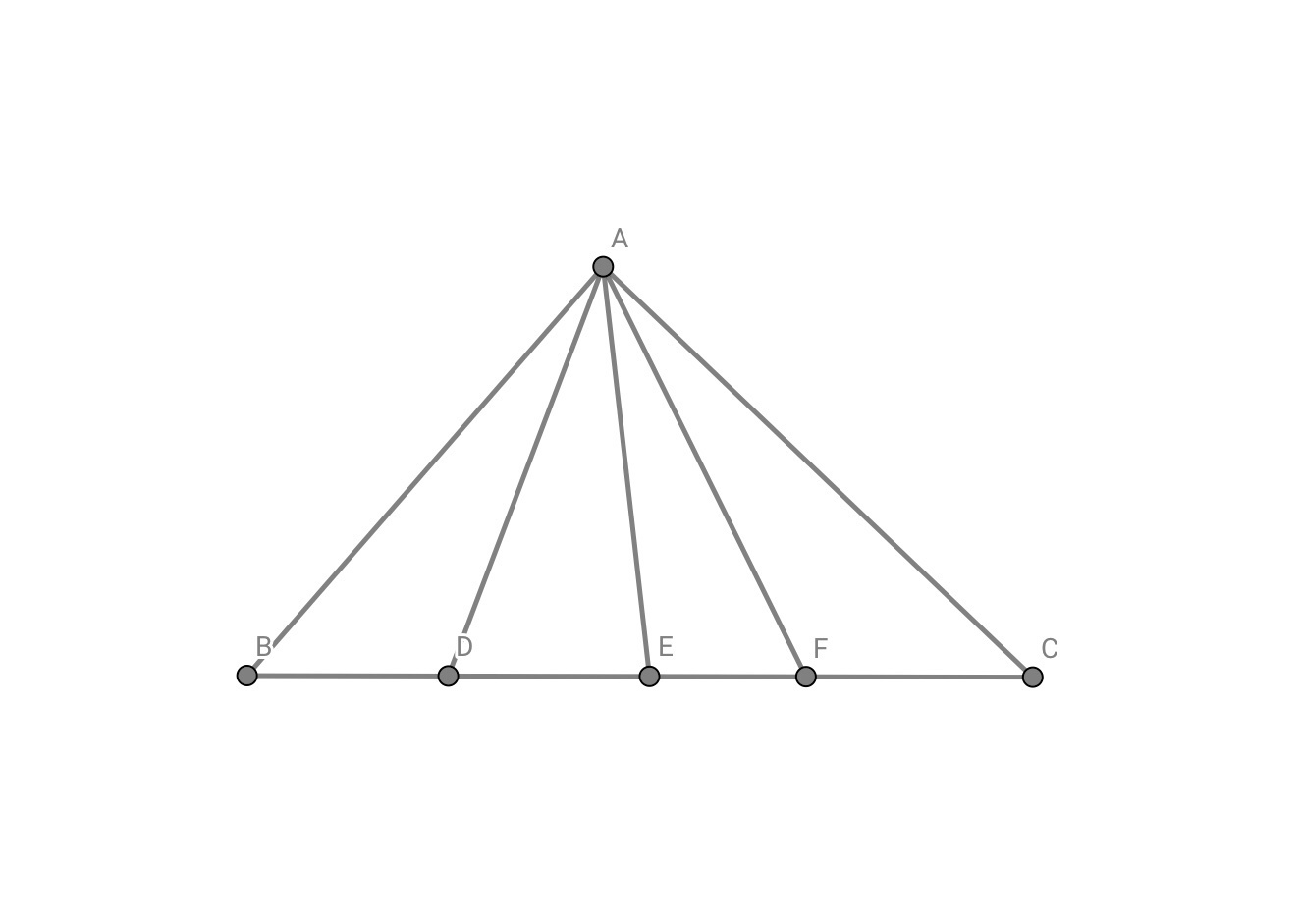 In
△
A
B
C
,
D
,
E
,
F
are three points on
B
C
.We know that
∠
B
A
C
=
1
0
0
∘
,
∠
C
A
F
=
2
0
∘
,
A
B
=
A
C
,
F
C
B
D
=
E
F
D
E
,
∠
D
A
F
=
∠
B
A
D
+
∠
C
A
F
,What’s the measurement of
∠
D
A
E
in degrees?
In
△
A
B
C
,
D
,
E
,
F
are three points on
B
C
.We know that
∠
B
A
C
=
1
0
0
∘
,
∠
C
A
F
=
2
0
∘
,
A
B
=
A
C
,
F
C
B
D
=
E
F
D
E
,
∠
D
A
F
=
∠
B
A
D
+
∠
C
A
F
,What’s the measurement of
∠
D
A
E
in degrees?
The answer is 30.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Call ∠ B A D = θ so ∠ D A F = θ + 2 0 ∘ . Also because △ A B C is isoscles, ∠ A B C = ∠ A C B = 4 0 ∘
Then we can find exterior angles ∠ A D E = 4 0 ∘ + θ and ∠ A F E = 6 0 ∘ , so in △ D A F , ∠ D A F = 8 0 ∘ − θ .
Equating the two formulas for ∠ D A F gives θ = 3 0 ∘ and also ∠ D A F = 5 0 ∘ . A few other angles can also be easily derived from angles of a triangle sum to 1 8 0 ∘ , but not the one we want.
Apply the law of sines on △ B A D and △ C A F which have an equal side and can be combined. Calling F C B D = E F D E = a allows us to solve for a .
a = sin 2 0 ∘ sin 1 1 0 ∘ sin 3 0 ∘ sin 1 2 0 ∘
Call ∠ D A E = α so ∠ A E F = ( 5 0 ∘ − α ) then apply the law of sines on these two triangles which have a side in common. Combine as before but this time rewrite the result as
sin ( 5 0 ∘ − α ) sin α = sin 6 0 ∘ a sin 7 0 ∘
Finally, substitute a into this and reduce, since sin 7 0 ∘ = sin 1 1 0 ∘ and sin 1 2 0 ∘ = sin 6 0 ∘ and you're left with
sin ( 5 0 ∘ − α ) sin α = sin 2 0 ∘ sin 3 0 ∘
So, by inspection α = ∠ D A E = 3 0 ∘
In the first line I think you meant ∠ A B C = ∠ A C B = 4 0 °
Given < BAC = 100, AB = AC implies that <ACF = < ABD = 40. Since <CAF = 20, < AFC = 120, < AFE = 60. Let x = <BAD. Then <DAF = x + 20.In triangle DAF, < ADF = 100 - x, and < BDA = 80 + x. Then in triangle ABD, 180 = x + 40 + 80 + x, or 180 = 2x + 120, and x = 30.Then <DAF = 100 - 30 - 20 = 50 = x + 20, so <DAE = 30. Ed Gray
By angle addition, ∠ B A C = ∠ B A D + ∠ D A F + ∠ C A F , and since we are given that ∠ B A C = 1 0 0 ° and ∠ C A F = 2 0 ° , ∠ B A D + ∠ D A F = 8 0 ° . We are also given that ∠ D A F = ∠ B A D + ∠ C A F , so ∠ D A F = ∠ B A D + 2 0 ° . Solving these two formulas gives ∠ D A F = 5 0 ° a n d ∠ B A D = 3 0 ° .
Since A B = A C and ∠ D A F = ∠ B A D + ∠ C A F , we can make a folds on segment A D and A F such that B ′ and C ′ meet at the same point G , as shown below.
Let H be the intersection of D F and A G . Since ∠ A C F = ∠ A B D (from isosceles △ A B C ), ∠ A G F = ∠ D G A , and by triangle ratios F G D G = H F D H . Since G D = B D and F G = F C by reflection, F C B D = H F D H . Since we are given that F C B D = E F D E , E is the same point as H .
Therefore, since ∠ D A E = ∠ B A D by reflection, ∠ D A E = ∠ B A D = 3 0 ° .