The sane Functional equation again

As $f(n)$ increases with $n$ , $f(1)$ has the smallest value. Assume that $f(1) = 1$ , but from $f(f(n)) = 3n$ we have $f(f(1)) = f(1) = 3$ , which contradict with $f(1) = 1$ , hence $f(1) \ne 1$ . Assume that $f(1) = 3$ , then $f(f(1)) = f(3) = 3$ $\implies f(1)=f(3)=3$ , which is unacceptable as $f(n)$ is an increasing function. Therefore, $f(1) = 2$ . Then we have:

$\begin{aligned} f(1) & = 2 \\ f(f(1)) & = f(2) = 3 \\ f(f(2)) & = f(3) = 6 \\ f(f(3)) & = f(6) = 9 \\ f(f(6)) & = f(9) = 18 \\ f(f(9)) & = f(18) = 27 \end{aligned}$

We note that $f(3)=6$ and $f(6) = 9$ and $f(n) \in \mathbb N$ is increasing, it must be $f(4)=7$ and $f(5)=8$ as $\underbrace{f(3)}_{=6} < \color{#3D99F6}{\underbrace{f(4)}_{=7} < \underbrace{f(5)}_{=8}} < \underbrace{f(6)}_{=9}$ .

And we further have:

$\begin{aligned} f(4) & = \color{#3D99F6}{7} & \implies \color{#3D99F6}{x_1 = 4} \\ f(5) & = 8 \\ f(f(4)) & = f(7) = \color{#3D99F6}{12} & \implies \color{#3D99F6}{x_2 = 7} \\ f(f(5)) & = f(8) = 15 \\ f(f(7)) & = f(12) = \color{#3D99F6}{21} & \implies \color{#3D99F6}{x_3 = 12} \\ f(f(8)) & = f(15) = 24 \end{aligned}$

Again $\underbrace{f(15)}_{=24} < \color{#3D99F6}{\underbrace{f(16)}_{=25} < \underbrace{f(17)}_{=26}} < \underbrace{f(18)}_{=27}$ , $\implies f(17) = \color{#3D99F6}{26}$ $\implies \color{#3D99F6}{x_4 = 17}$ .

$\implies x_1+x_2+x_3+x_4 = 4+7+12+17 = \boxed{40}$

We know that there can be no fixed points for this function, or else $x=f(x) \implies x=f(x)=f(f(x))=3x \implies x=0 \notin \mathbb {N}.$

So, $f(1) > 1.$ Note that if $f(1)\geq 3$ , we also contradict ourselves: we know $f(f(1))=3$ and $f(x)\geq f(1) \geq 3, \forall x \geq 3.$ Since there are no fixed points, this implies that $f(f(1)) > 3$ , a contradiction.

It follows that $f(1)=2$ , from which we see that $f(2)=f(f(1))=3.$ Following similar logic leads to a (unique!) sequence that defines this function from the naturals to themselves.

Great question!

Here is a nice closed form for $f$ . Let $n \in \mathbb{N}$ and find the largest integer $k$ such that $3^k < n$ . We can write $n = 3^k + r \quad \text{or} \quad n = 2\cdot 3^k + r,$ with $0 \leq r < 3^k$ , and this representation is unique. Define $f$ by $f(n) = \begin{cases} 2 \cdot 3^k + r & n = 3^k + r, \\ 3^{k + 1} + 3r & n = 2 \cdot 3^k + r.\end{cases} \tag{1}$ The graph below shows $f$ is indeed increasing, and we can directly compute $f(f(n))$ when $n = 3^k + r$ and $2\cdot 3^k + r$ to see that that $f(f(n)) = 3n$ .

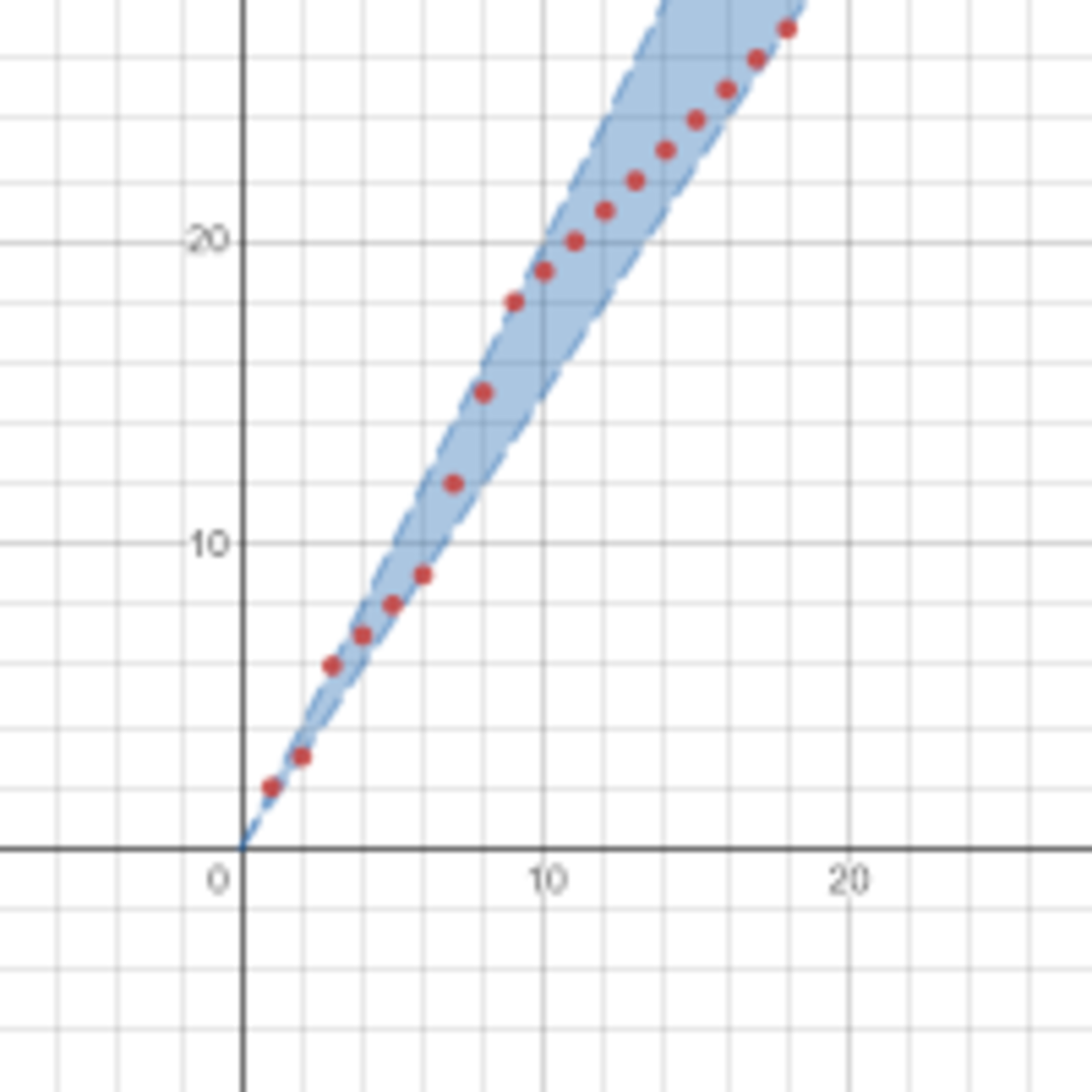
We claim that, if $f$ is increasing and $f(f(n)) = 3n$ , then $(1)$ holds for all $n = 3^k + r$ and $n = 2 \cdot 3^k + r$ . To prove this, we will start by letting $r = 0$ . If $k = 0$ , then $n = 1$ or $2$ . Other solutions have already shown that $f(1) = 2$ and $f(2) = 3$ , and we can see directly that $(1)$ holds. Fix $k \geq 0$ and suppose that $(1)$ holds when $n = 3^k$ and $2 \cdot 3^k$ : $f(3^k) = 2 \cdot 3^k \quad \text{and} \quad f(2 \cdot 3^k) = 3^{k + 1}.$ Apply the functional equation twice to the equation on the right to obtain $f(f(2 \cdot 3^k)) = f(3^{k + 1}) = 2 \cdot 3^{k + 1} \quad \text{and} \quad f(f(3^{k + 1})) = f(2 \cdot 3^{k + 1}) = 3^{k + 2}.$ This shows $(1)$ holds for $n = 3^{k + 1}$ and $n = 2 \cdot 3^{k + 1}$ , so by induction, for $k \geq 0$ , $f(3^k) = 2 \cdot 3^k \quad \text{and} \quad f(2 \cdot 3^k) = 3^{k + 1}. \tag{2}$ Now let $r \in \{1,2,\dots,3^k - 1\}$ . Either $n = 3^k + r$ or $n = 2 \cdot 3^k + r$ . If $n = 3^k + r$ , then we have $3^k < n < 2 \cdot 3^k$ . Samrat Mukhopadhyay has already observed that $f$ must be strictly increasing, so $(2)$ implies $f(3^k) = 2 \cdot 3^k < f(n) < 3^{k + 1} = f(2 \cdot 3^k).$ In other words, $f$ maps $\{3^k + r: 0 < r < 3^k\}$ into $\{2 \cdot 3^k + r : 0 < r < 3^k\}$ . But $f$ is strictly increasing, so this is only possible if $f(3^k + r) = 2\cdot 3^k + r. \tag{3}$ If instead $n = 2 \cdot 3^k + r$ , then by $(3)$ $f(3^k + r) = 2 \cdot 3^k + r = n,$ and by the functional equation, $f(f(3^k + r)) = f(n) = 3(3^k + r) = 3^{k + 1} + 3r. \tag{4}$ From $(2)$ , $(3)$ , and $(4)$ , we conclude that $(1)$ holds for all $n$ .